题目内容
(本小题满分13分)已知数列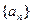 ,定义其倒均数是
,定义其倒均数是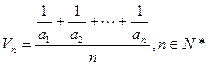 。
。
(1)求数列{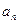 }的倒均数是
}的倒均数是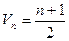 ,求数列{
,求数列{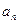 }的通项公式
}的通项公式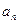 ;
;
(2)设等比数列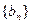 的首项为-1,公比为
的首项为-1,公比为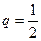 ,其倒数均为
,其倒数均为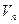 ,若存在正整数k,使
,若存在正整数k,使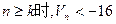 恒成立,试求k的最小值。
恒成立,试求k的最小值。
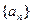 ,定义其倒均数是
,定义其倒均数是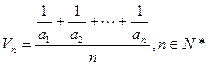 。
。(1)求数列{
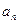 }的倒均数是
}的倒均数是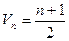 ,求数列{
,求数列{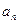 }的通项公式
}的通项公式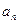 ;
;(2)设等比数列
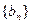 的首项为-1,公比为
的首项为-1,公比为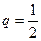 ,其倒数均为
,其倒数均为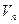 ,若存在正整数k,使
,若存在正整数k,使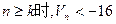 恒成立,试求k的最小值。
恒成立,试求k的最小值。(1)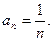
(2)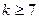 时均适合题意,即K的最小值为7。
时均适合题意,即K的最小值为7。
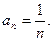
(2)
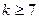 时均适合题意,即K的最小值为7。
时均适合题意,即K的最小值为7。(1)依题意,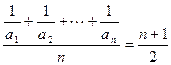
即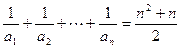 …………………2分
…………………2分
当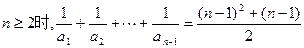
两式相减得,得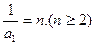 ∴
∴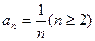 ……………………4分
……………………4分
当n=1时,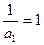 ∴
∴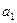 =1适合上式…………………5分
=1适合上式…………………5分
故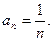 …………………………6分
…………………………6分
(2)由题意,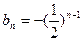 ∴
∴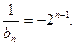 …………….. 8分
…………….. 8分
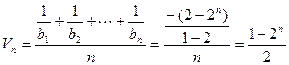 ………………10分
………………10分
不等式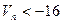 恒成立,即
恒成立,即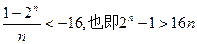 恒成立。…………12分
恒成立。…………12分
经检验: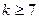 时均适合题意,即K的最小值为7。……………………13分
时均适合题意,即K的最小值为7。……………………13分
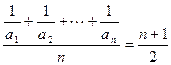
即
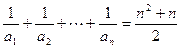 …………………2分
…………………2分当
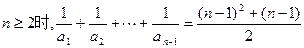
两式相减得,得
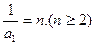 ∴
∴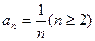 ……………………4分
……………………4分当n=1时,
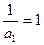 ∴
∴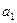 =1适合上式…………………5分
=1适合上式…………………5分故
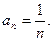 …………………………6分
…………………………6分(2)由题意,
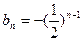 ∴
∴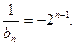 …………….. 8分
…………….. 8分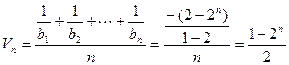 ………………10分
………………10分不等式
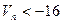 恒成立,即
恒成立,即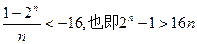 恒成立。…………12分
恒成立。…………12分经检验:
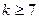 时均适合题意,即K的最小值为7。……………………13分
时均适合题意,即K的最小值为7。……………………13分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
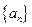 满足:
满足: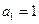 ,且当
,且当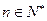 时,
时,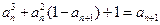 .
.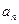 与
与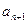 的大小,并证明你的结论.
的大小,并证明你的结论.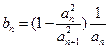 ,其中
,其中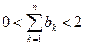 .
.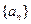 满足
满足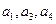 成等比数列,
成等比数列,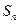 为数列
为数列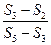 的值为 ( )
的值为 ( )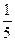
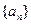 中,
中,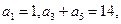 其前n项和
其前n项和 ,则n=__
,则n=__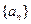 的前四项依次为
的前四项依次为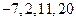 的一个通项公式是 ( )
的一个通项公式是 ( )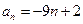
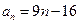
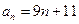
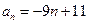
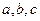 成等差数列,且
成等差数列,且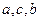 成等比数列,则
成等比数列,则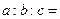 _________
_________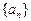 为等差数列,
为等差数列,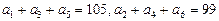 ,以
,以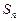 表示
表示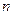 项和,则使
项和,则使 n}的通项公式
n}的通项公式