题目内容
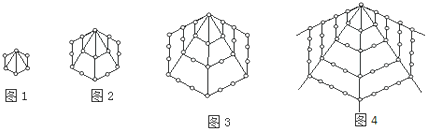
10．
将棱长相等的正方体按右图所示的形状摆放，从上往下依次为第1层，第2层，第3层，…，则第n层正方体的个数是$\frac{n（n+1）}{2}$．
分析 先设上往下各层的正方体数目组成数列{an}，再观察图形得出：a2-a1=2，a3-a2=3…an-an-1=n．最后利用叠加法求出数列的通项公式．
解答 解：设上往下各层的正方体数目组成数列{an}
由题得：a2-a1=2，
a3-a2=3
…
an-an-1=n．
把上面各式相加得：an-a1=2+3+4+…+n
所以an=a1+2+3+…+n=1+2+3+…+n=$\frac{n（n+1）}{2}$．
故答案为：$\frac{n（n+1）}{2}$．
点评 本题主要考查数列的应用问题．解决本题的关键在于观察出数列各项之间的关系，再结合叠加法求出数列的通项公式．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
15．下列不等式中恒成立的是（ ）
| A． | $2-x-\frac{4}{x}$≤-2 | B． | $sinx+\frac{1}{sinx}$≥2 | C． | $\frac{{{x^2}+5}}{{\sqrt{{x^2}+4}}}$≥2 | D． | $\frac{{{x^2}+2}}{{\sqrt{{x^2}+2}}}$≥$\sqrt{2}$ |
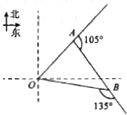如图，一只蜘蛛从点O出发沿北偏东45°方向爬行xcm，到达点A处捕捉到一只小虫，然后沿OA方向右转105°爬行10cm，到达点B处捕捉哦另一只小虫，这时他沿AB方向右转135°爬行回到它的出发点O处，那么x=$\frac{10\sqrt{6}}{3}$．
13．函数y=x3+4x的递增区间是（ ）
| A． | （0，+∞） | B． | （-∞，-2） | C． | （2，+∞） | D． | （-∞，+∞） |
