题目内容
17.已知x2+y2=1,求证:|x2+2xy-y2|≤$\sqrt{2}$.分析 由条件利用三角代换化简不等式的左边为|$\sqrt{2}$sin($\frac{π}{4}$+2θ)|,再根据正弦函数的值域,证得不等式成立.
解答 解:∵x2+y2=1,∴可令x=cosθ,y=sinθ,
∴|x2+2xy-y2|=|cos2θ-sin2θ+2sinθcosθ|=|cos2θ+sin2θ|=|$\sqrt{2}$sin($\frac{π}{4}$+2θ)|≤$\sqrt{2}$,
故:|x2+2xy-y2|≤$\sqrt{2}$成立.
点评 本题主要考查三角代换,两角和的正弦公式、正弦函数的值域,属于基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
8.已知复数z=$\frac{2+ai}{5-i}$是纯虚数,则实数a的值为( )
| A. | 8 | B. | 10 | C. | 6 | D. | 12 |
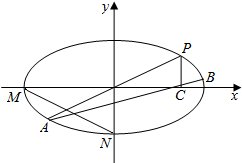 如图,在平面直角坐标系xOy中,M、N分别是椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,设直线PA的斜率为k.
如图,在平面直角坐标系xOy中,M、N分别是椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,设直线PA的斜率为k.