题目内容
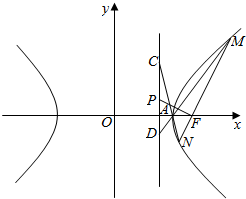
19.过抛物线x2=4y的焦点F作直线l交抛物线于A,B两点,则弦AB的中点M的轨迹方程是y=$\frac{1}{2}$x2+1.分析 将直线方程代入到抛物线方程,利用中点坐标公式,再消参即可.
解答 解:设直线方程可以写成 y=k•x+1代入抛物线方程,得到0.25x2-kx-1=0,
所以中点坐标xm=0.5(x1+x2)=2k,
ym=0.5(y1+y2)=0.5(kx1+kx2+2)=0.5k(x1+x2)+1=kxm+1=$\frac{{{x}_{m}}^{2}}{2}$+1,
所以轨迹方程就是y=$\frac{1}{2}$x2+1,
故答案为:y=$\frac{1}{2}$x2+1.
点评 本题主要考查直线与抛物线的位置关系,考查轨迹问题,属于中档题.

练习册系列答案
相关题目
4.已知在△ABC中,a、b、c分别是三内角∠A、∠B、∠C的对边,且$\frac{\sqrt{2}b}{a-\sqrt{2}b}$=$\frac{sin2B}{sinA-sin2B}$,则∠B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |