Question

12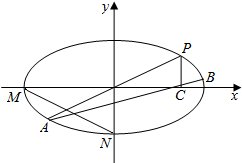．如图，在平面直角坐标系xOy中，M、N分别是椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$的顶点，过坐标原点的直线交椭圆于P，A两点，其中点P在第一象限，过P作x轴的垂线，垂足为C，设直线PA的斜率为k．
（1）若直线PA平分线段MN，求k的值；
（2）求△PMN，面积S的最大值，并指出对应的点P的坐标；
（3）对任意的k＞0，过点P作PA的垂线交椭圆于B，求证：A，C，B三点共线．

Answer 1

分析 （1）由题设写出点M，N的坐标，求出线段MN中点坐标，根据线PA过原点和斜率公式，即可求出k的值；
（2）写出与MN所在直线平行的直线方程，与椭圆方程联立，利用判别式等于0求出与MN所在直线平行且与椭圆相切的直线方程，进一步求出P的坐标及P到直线MN的距离，代入三角形面积公式得答案；
（3）设PB中点Q（x₀，y₀），利用点差法得到${k}_{PB}=-\frac{{x}_{0}}{2{y}_{0}}$，由PA⊥PB，得到${k}_{OQ}=\frac{{y}_{0}}{{x}_{0}}=\frac{k}{2}$．然后结合PO=OA，PQ=QB，可得${k}_{AB}=\frac{k}{2}$．再求出${k}_{AC}=\frac{k}{2}$得A，C，B三点共线．

解答 （1）解：由题设知，a=2，b=$\sqrt{2}$，
故M（-2，0），N（0，-$\sqrt{2}$），
∴线段MN中点坐标为（-1，-$\frac{\sqrt{2}}{2}$）．
由于直线PA平分线段MN，故直线PA过线段MN的中点，又直线PA过原点，
∴k=$\frac{\sqrt{2}}{2}$；
（2）解：∵M（-2，0），N（0，-$\sqrt{2}$），∴${k}_{MN}=\frac{-\sqrt{2}-0}{0-（-2）}=-\frac{\sqrt{2}}{2}$，
设与MN平行的直线方程为y=$-\frac{\sqrt{2}}{2}x+m$，
联立$\left\{\begin{array}{l}{y=-\frac{\sqrt{2}}{2}x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$，得${x}^{2}-\sqrt{2}mx+{m}^{2}-2=0$．
由△=$（-\sqrt{2}m）^{2}-4{m}^{2}+8=0$，解得：m=±2．
由题意可知，当m=2时，直线$y=-\frac{\sqrt{2}}{2}x+2$与直线MN的距离最大，
最大值d=$\frac{|-4|}{\sqrt{（\sqrt{2}）^{2}+{2}^{2}}}=\frac{2\sqrt{6}}{3}$．
即△PMN面积S有最大值，等于$\frac{1}{2}|MN|d$=$\frac{1}{2}×\sqrt{6}×\frac{2\sqrt{6}}{3}=2$．
由${x}^{2}-2\sqrt{2}x+2=0$，解得x=$\sqrt{2}$，y=1．
∴P点坐标为（$\sqrt{2}，1$）；
（3）证明：设P（x₁，y₁），B（x₂，y₂），PB中点Q（x₀，y₀），
则$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}=1$，$\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{2}=1$，
两式作差可得：$\frac{（{x}_{1}-{x}_{2}）（{x}_{1}+{x}_{2}）}{4}=-\frac{（{y}_{1}-{y}_{2}）（{y}_{1}+{y}_{2}）}{2}$，
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{{x}_{0}}{2{y}_{0}}$，即${k}_{PB}=-\frac{{x}_{0}}{2{y}_{0}}$．
∵PA⊥PB，∴k$•（-\frac{{x}_{0}}{2{y}_{0}}）=-1$，即$\frac{{y}_{0}}{{x}_{0}}=\frac{k}{2}$．
∴${k}_{OQ}=\frac{{y}_{0}}{{x}_{0}}=\frac{k}{2}$．
∵PO=OA，PQ=QB，
∴OQ∥AB，即${k}_{AB}=\frac{k}{2}$．
∵${k}_{AC}=\frac{{y}_{A}-0}{{x}_{A}-{x}_{C}}=\frac{-{y}_{1}-0}{-{x}_{1}-{x}_{1}}=\frac{{y}_{1}}{2{x}_{1}}=\frac{k}{2}$．
∴k_AC=k_AB．
故A，C，B三点共线．

点评 此题是个难题．考查椭圆的标准方程和简单的几何性质，以及直线斜率的求法，考查直线与椭圆的位置关系，体现了方程的思想和数形结合思想，同时也考查了学生观察、推理以及创造性地分析问题、解决问题的能力．