题目内容
20.若$sin(π+α)=\frac{3}{5}$,α是第三象限的角,则tanα=$\frac{3}{4}$则$\frac{{sin\frac{π+α}{2}-cos\frac{π+α}{2}}}{{sin\frac{π-α}{2}-cos\frac{π-α}{2}}}$=-$\frac{1}{2}$.分析 由诱导公式可得sinα=-$\frac{3}{5}$,结合α是第三象限的角,利用同角三角函数基本关系的运用可得cosα,将所求由诱导公式化简可得$\frac{1+sinα}{cosα}$,即可求值.
解答 解:∵$sin(π+α)=\frac{3}{5}$,
∴sinα=-$\frac{3}{5}$,
∵α是第三象限的角,可得cos$α=-\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,
∴$\frac{{sin\frac{π+α}{2}-cos\frac{π+α}{2}}}{{sin\frac{π-α}{2}-cos\frac{π-α}{2}}}$=$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$=$\frac{(cos\frac{α}{2}+sin\frac{α}{2})^{2}}{co{s}^{2}\frac{α}{2}-si{n}^{2}\frac{α}{2}}$=$\frac{1+sinα}{cosα}$=$\frac{1-\frac{3}{5}}{-\frac{4}{5}}$=-$\frac{1}{2}$.
故答案为:$\frac{3}{4}$,-$\frac{1}{2}$.
点评 本题主要考查了运用诱导公式化简求值,同角三角函数基本关系的运用,考查了计算能力,属于基本知识的考查.

练习册系列答案
相关题目
5.y=$\frac{{x}^{2}}{x+3}$的导数是( )
| A. | $\frac{{x}^{2}-6x}{(x+3)^{2}}$ | B. | $\frac{{x}^{2}+6x}{x+3}$ | C. | $\frac{{x}^{2}}{(x+3)^{2}}$ | D. | $\frac{{x}^{2}+6x}{(x+3)^{2}}$ |
12.函数y=$\frac{1}{2}$(ex+e-x)的导数是( )
| A. | $\frac{1}{2}$(e x-e -x) | B. | $\frac{1}{2}$(e x+e -x) | C. | e x-e -x | D. | e x+e -x |
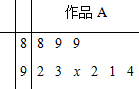 我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.