题目内容
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在 ,(单位:元).
,(单位:元).
(Ⅰ)估计居民月收入在 的概率;
的概率;
(Ⅱ)根据频率分布直方图估计样本数据的中位数;
(Ⅲ)若将频率视为概率,从本地随机抽取3位居民(看做有放回的抽样),求月收入在 的居民数X的分布列和数学期望.
的居民数X的分布列和数学期望.
(1)0.2;(2)2400;(3)分布列详见解析,0.9.
解析试题分析:(1)由频率分布直方图求概率;(2)利用频率分布直方图求中位数;(3)利用二项分布,求每一种情况的概率,列出分布列,求数学期望.
试题解析:(Ⅰ)由题意,居民月收入在 的概率约为
的概率约为 . 2分
. 2分
(Ⅱ)由频率分布直方图知,中位数在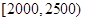 ,
,
设中位数为 ,则
,则 ,解得
,解得 .6分
.6分
(Ⅲ)居民月收入在 的概率为
的概率为 ,
,
由题意知, ,
,
因此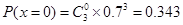 ,
, ,
, ,
, 10分
10分
故随机变量 的分布列为
的分布列为 X 0 1 2 3 P 0.343 0.441 0.189 0.027  的数学期望为
的数学期望为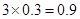 . 12分
. 12分
考点:1.频率分步直方图;2.中位数;3.分布列;4.数学期望;5.二项分布.

某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在(2)中抽取的40名学生中,要随机选取2名学生参 加座谈会,记“其中成绩为优秀的人数”为X,求X的分布列与数学期望.
从某学校高三年级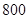 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组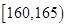 ; 第八组
; 第八组 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图. 
(1)根据已知条件填写下面表格:
| 组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 样本数 | | | | | | | | |
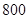 名学生中身高在
名学生中身高在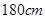 以上(含
以上(含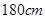 )的人数;
)的人数;(3)在样本中,若第二组有
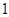 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有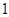 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少? 2013年1月份,我国北方部分城市出现雾霾天气,形成雾霾天气主要原因与 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
 日均值k(微克) 日均值k(微克) | 空气质量等级 |
 | 一级 |
 | 二级 |
 | 超标 |

某环保部门为了了解甲、乙两市的空气质量状况,在过去某月的30天中分别随机抽取了甲、乙两市6天的
 日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市
日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市 日均值的样本平均数,并由此判断哪个市的空气质量较好;
日均值的样本平均数,并由此判断哪个市的空气质量较好;(Ⅱ)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量超标的概率.

 其中
其中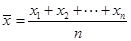

 ℃为低热,
℃为低热, ℃为中等热,
℃为中等热, ℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率. 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图: ,求
,求 .
.

 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。

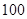 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组 ;……,第九组
;……,第九组 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。 千克以上(含
千克以上(含 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整; 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为 ,求
,求 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为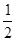 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区