题目内容
(在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如下茎叶图所示: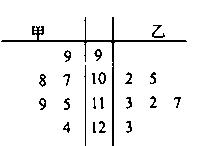
(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(II)从乙的6次培训成绩中随机选择2个,记被抽到的分数超过115分的个数为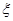 ,试求
,试求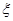 的分布列和数学期望.
的分布列和数学期望.
(I)选择乙;(II)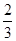 .
.
解析试题分析:(I)根据茎叶图,写出两个同学的成绩,对于这两个同学的成绩求出平均数,结果两人的平均数相等,再比较两个人的方差,得到乙的方差较小,这样可以派乙去,因为乙的成绩比较稳定.(II)由题意知本题是一个古典概型,试验发生包含的所有事件是从乙的6次培训成绩中随机选择2个,满足事件的恰好有2次,记被抽到的分数超过115分的个数为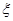 ,由题意值
,由题意值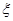 可取0,1,2,根据古典概型的概率公式求出对应的概率,写出分布列,求出期望.
可取0,1,2,根据古典概型的概率公式求出对应的概率,写出分布列,求出期望.
试题解析:(I)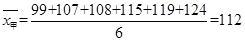 ;
;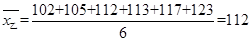 .
.
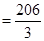
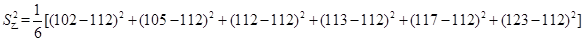
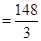
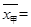
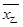 ;
;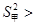
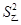 .
.
所以,甲乙两方的平均水平一样,乙的方差小,乙发挥的更稳定,则选择乙.
(II)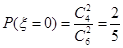 ;
; 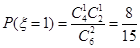 ;
;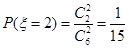 .
.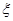 的分布列为:
的分布列为:
所以数学期望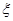
0 1 2 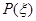
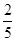
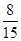
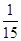
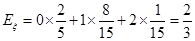 .
.
考点:1.茎叶图;2.平均数与方差;3.离散型随机变量及其分布列;4.期望.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 | 候车时间 | 人数 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在(2)中抽取的40名学生中,要随机选取2名学生参 加座谈会,记“其中成绩为优秀的人数”为X,求X的分布列与数学期望.
某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 颗 颗 | 23 | 25 | 30 | 26 | 16 |
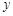 关于
关于 的线性回归方程
的线性回归方程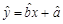 ;
;(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅰ)中所得的线性回归方程是否可靠?
(参考公式:
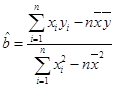
 ,
, )
)(参考数据:
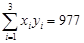 ,
, )
) 


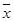 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的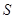 大小为多少?并说明
大小为多少?并说明


 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图; 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 之间的概率.
之间的概率.
 其中
其中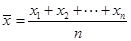

 ℃为低热,
℃为低热, ℃为中等热,
℃为中等热, ℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率. 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。

 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组 ;……,第九组
;……,第九组 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。 千克以上(含
千克以上(含 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整; 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为 ,求
,求