题目内容
某校有教职工 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
(Ⅰ)随机抽取一人,是35岁以下的概率为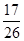 ,求
,求 的值;
的值;
(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
(Ⅰ) ,
, ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)先根据已知条件“随机抽取一人,是35岁以下的概率为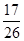 ”,得到
”,得到 ,解出
,解出 的值,再由总人数减去已知的所有的人数即是未知的
的值,再由总人数减去已知的所有的人数即是未知的 的值;(Ⅱ)将
的值;(Ⅱ)将 岁以上的
岁以上的 人进行编号,列举出所有满足“从这
人进行编号,列举出所有满足“从这 人中任取
人中任取 人”和“其中恰好有一位研究生”的基本事件的个数,然后求出“从50岁以上的6人中随机抽取两人,恰好只有一位是研究生”的概率.
人”和“其中恰好有一位研究生”的基本事件的个数,然后求出“从50岁以上的6人中随机抽取两人,恰好只有一位是研究生”的概率.
试题解析:(Ⅰ)由已知得: ,解得
,解得 ,
,
故 ,即
,即 .
.
(Ⅱ)将 岁以上的
岁以上的 人进行编号:四位本科生为:
人进行编号:四位本科生为: ,两位研究生为
,两位研究生为 .
.
从这 人中任取
人中任取 人共有
人共有 种等可能发生的基本事件,分别为:
种等可能发生的基本事件,分别为: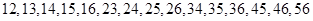 ,
,
其中恰好有一位研究生的有 种,分别为:
种,分别为: ,
,
故所求的概率为: .
.
考点:1.简单随机抽样;2.基本事件;3.随机事件的概率

城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的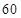 名候车乘客中随机抽取
名候车乘客中随机抽取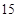 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |  |  |
| 二 |  | 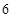 |
| 三 |  |  |
| 四 |  |  |
| 五 |  |  |
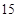 名乘客的平均候车时间;
名乘客的平均候车时间;(2)估计这
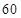 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;(3)若从上表第三、四组的
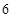 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率. 用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 99 | 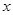 |
| 高二 | 27 | 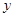 |
| 高三 | 18 | 2 |
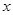 ,
,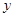 ;
;(Ⅱ)若从高二、高三年级抽取的人中选
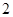 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率. 某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在(2)中抽取的40名学生中,要随机选取2名学生参 加座谈会,记“其中成绩为优秀的人数”为X,求X的分布列与数学期望.
某年青教师近五年内所带班级的数学平均成绩统计数据如下:
年份 年 年 | 2009 | 2010 | 2011 | 2012 | 2013 |
平均成绩 分 分 | 97 | 98 | 103 | 108 | 109 |
 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。(2)利用(1)中所求出的直线方程预测该教师2014年所带班级的数学平均成绩.

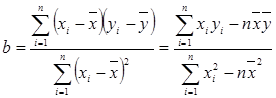


从某学校高三年级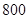 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组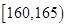 ; 第八组
; 第八组 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图. 
(1)根据已知条件填写下面表格:
| 组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 样本数 | | | | | | | | |
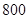 名学生中身高在
名学生中身高在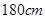 以上(含
以上(含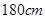 )的人数;
)的人数;(3)在样本中,若第二组有
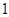 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有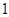 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少? 


 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图; 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 之间的概率.
之间的概率.