题目内容
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.
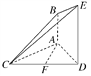
(1)求证:AF∥平面BCE;
(2)判断平面BCE与平面CDE的位置关系,并证明你的结论.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)取CE中点M,根据平几知识可得四边形BAFM为平行四边形,即得BM//AF,再根据线面平行判定定理得结论(2)先根据空间直角坐标系,再设立各点坐标,根据方程组解得平面法向量,根据法向量相互垂直得平面BCE与平面CDE垂直.
试题解析: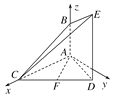
建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),C(2a,0,0),B(0,0,a),D(a,![]() a,0),E(a,
a,0),E(a,![]() a,2a).
a,2a).
因为F为CD的中点,
所以F![]() .
.
(1)证明:![]() =
=![]() ,
,![]() =(a,
=(a,![]() a,a),
a,a),![]() =(2a,0,-a).
=(2a,0,-a).
因为![]() =
=![]() (
(![]() +
+![]() ),AF平面BCE,所以AF∥平面BCE.
),AF平面BCE,所以AF∥平面BCE.
(2)平面BCE⊥平面CDE.证明如下:
因为![]() =
=![]() ,
,![]() =(-a,
=(-a,![]() a,0),
a,0),![]() =(0,0,-2a),所以
=(0,0,-2a),所以![]() ·
·![]() =0,A
=0,A![]() ·
·![]() =0,所以
=0,所以![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,所以AF⊥平面CDE,
,所以AF⊥平面CDE,
又AF∥平面BCE,所以平面BCE⊥平面CDE.

练习册系列答案
相关题目