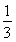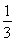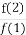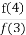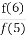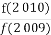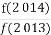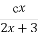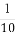题目内容
袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
(1) (2)
(2)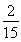
【解析】(1)若编号为n的球的重量大于其编号,
则n2-6n+12>n,即n2-7n+12>0.
解得n<3或n>4.所以n=1,2,5,6.
所以从袋中任意取出一个球,其重量大于其编号的概率P= =
= .
.
(2)不放回地任意取出2个球,这2个球编号的所有可能情形为:
1,2;1,3;1,4;1,5;1,6;
2,3;2,4;2,5;2,6;
3,4;3,5;3,6;
4,5;4,6;
5,6.
共有15种可能的情形.
设编号分别为m与n(m,n∈{1,2,3,4,5,6},且m≠n)球的重量相等,则有
m2-6m+12=n2-6n+12,即有(m-n)(m+n-6)=0.
所以m=n(舍去),或m+n=6.
满足m+n=6的情形为1,5;2,4,共2种情形.
故所求事件的概率为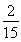 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目