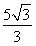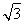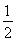题目内容
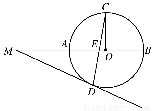
如图，在几何体ABCDE中，AB＝AD＝2，AB⊥AD，AE⊥平面ABD，M为线段BD的中点，MC∥AE，且AE＝MC＝
.
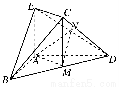
(1)求证：平面BCD⊥平面CDE；
(2)若N为线段DE的中点，求证：平面AMN∥平面BEC.
（1）见解析（2）见解析
【解析】(1)证明：∵AB＝AD＝2，AB⊥AD，M为线段BD的中点，
∴AM＝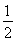
BD＝
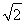，AM⊥BD，
∵AE＝MC＝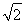
，
∴AE＝MC＝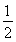
BD＝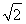
，
∴BC⊥CD，BD⊥CM.
∵AE⊥平面ABD，MC∥AE，∴MC⊥平面ABD，
∴MC⊥AM，∴AM⊥平面CBD.
又MC∥AE，AE＝MC＝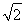
，
∴四边形AMCE为平行四边形，∴EC∥AM，
∴EC⊥平面CBD，∴BC⊥EC，
∵EC∩CD＝C，
∴BC⊥平面CDE.
∵BC?平面BCD，∴平面BCD⊥平面CDE.
(2)∵M为BD的中点，N为DE的中点，
∴MN∥BE.
由(1)知EC∥AM且AM∩MN＝M，
又BE∩EC＝E，
∴平面AMN∥平面BEC.
练习册系列答案
相关题目
