题目内容
13.已知定义在R上的函数f(x)=ln(e2x+1)+ax(a∈R)是偶函数.(1)求实数a的值;
(2)判断f(x)在[0,+∞)上的单调性,并用定义法证明;
(3)若f(x2+$\frac{1}{{x}^{2}}$)>f(mx+$\frac{m}{x}$)恒成立,求实数m的取值范围.
分析 (1)利用f(x)是定义在R上的偶函数,可得f(1)=f(-1),即可求出a.
(2)设x1,x2为[0,+∞)内的任意两个值,且x1<x2,利用函数的单调性的定义证明f(x1)-f(x2)<0,推出函数f(x)在[0,+∞)上是单调增函数.
(3)f(x)在[0,+∞)上是单调增函数,且是偶函数推出${x^2}+\frac{1}{x^2}>|{mx+\frac{m}{x}}|$,令$t=x+\frac{1}{x}$,则t∈(-∞,-2]∪[2,+∞),化简得到$|t|-\frac{2}{|t|}≥1$,|m|<1,求出-1<m<1.
解答 19.解:(1)因为f(x)是定义在R上的偶函数,所以f(1)=f(-1),
即ln(e2+1)+a=ln(e-2+1)-a,即2a=$ln\frac{{e}^{-2}+1}{{e}^{2}+1}$=-2,得a=-1,…2分
当a=-1时,f(x)=ln(e2x+1)-x,
对于?x∈R,f(-x)=ln(e-2x+1)+x=ln(e2x+1)-x=f(x),综上a=-1 …4分
(2)f(x)在[0,+∞)上是单调增函数,…5分
证明如下:
设x1,x2为[0,+∞)内的任意两个值,且x1<x2,则$f({x_1})-f({x_2})=ln({e^{2{x_1}}}+1)-{x_1}-ln({e^{2{x_2}}}+1)+{x_2}$=$ln(\frac{{{e^{2{x_1}}}+1}}{{{e^{2{x_2}}}+1}})+ln({e^{{x_2}-{x_1}}})=ln[\frac{{({e^{2{x_1}}}+1){e^{{x_2}-{x_1}}}}}{{{e^{2{x_2}}}+1}}]=ln(\frac{{{e^{{x_2}+{x_1}}}+{e^{{x_2}-{x_1}}}}}{{{e^{2{x_2}}}+1}})$
因为0≤x1<x2,所以x2-x1>0,x2+x1>0,所以${e^{{x_2}-{x_1}}}>1,{e^{{x_2}+{x_1}}}>1$,
所以${e^{{x_2}+{x_1}}}+{e^{{x_2}-{x_1}}}-({e^{2{x_2}}}+1)=(1-{e^{{x_2}-{x_1}}})({e^{{x_2}+{x_1}}}-1)<0$,所以${e^{{x_2}+{x_1}}}+{e^{{x_2}-{x_1}}}<({e^{2{x_2}}}+1)$,
所以$\frac{{{e^{{x_2}+{x_1}}}+{e^{{x_2}-{x_1}}}}}{{{e^{2{x_2}}}+1}}<1$,所以f(x1)-f(x2)<0,即f(x1)<f(x2),
所以f(x)在[0,+∞)上是单调增函数. …10分
(3)f(x)在[0,+∞)上是单调增函数,且是偶函数,又$f({x^2}+\frac{1}{x^2})>f(mx+\frac{m}{x})$,
所以${x^2}+\frac{1}{x^2}>|{mx+\frac{m}{x}}|$,…12分
令$t=x+\frac{1}{x}$,则t∈(-∞,-2]∪[2,+∞),
所以|mt|<t2-2,$|m|<|t|-\frac{2}{|t|}$恒成立,…14分
因为$|t|-\frac{2}{|t|}$,关于|t|在[2,+∞)上单调递增,
所以$|t|-\frac{2}{|t|}≥1$,所以|m|<1恒成立,所以-1<m<1.…16分.
点评 本题考查函数的恒成立,函数的单调性以及函数的奇偶性的综合应用,考查分析问题解决问题的能力.

 天天练口算系列答案
天天练口算系列答案| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{64}$=1 | D. | $\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{48}$=1 |
| A. | $\frac{1}{12}$ | B. | 12 | C. | $-\frac{1}{12}$ | D. | -12 |
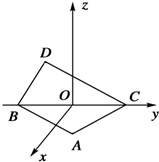 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则向量$\overrightarrow{AD}$的坐标为( )
如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则向量$\overrightarrow{AD}$的坐标为( )| A. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-1,$\frac{\sqrt{3}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) | D. | ($\frac{\sqrt{3}}{2}$,1,$\frac{\sqrt{3}}{2}$) |
| A. | -$\frac{48}{25}$ | B. | $\frac{48}{25}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |