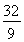题目内容
对定义域分别是Df，Dg的函数y＝f(x)，y＝g(x)，规定：函数h(x)＝
(1)若函数f(x)＝
，g(x)＝x2，写出函数h(x)的解析式；
(2)求问题(1)中函数h(x)的值域．
(1) h(x)＝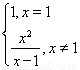
(2) h(x)值域(－∞，0]∪{1}∪[4，＋∞)
【解析】(1)Df＝{x|x≠1}，Dy＝R.
当x＝1时，h(x)＝x2＝1；
当x≠1时，h(x)＝f(x)g(x)＝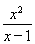
，
∴h(x)＝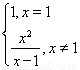
(2)当x＝1时，h(1)＝1；
当x≠1时，
方法一：h(x)＝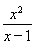
＝
＝x－1＋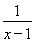
＋2；
当x＞1时，h(x)≥4，等号成立条件x＝2；
当x＜1时，h(x)＝－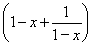
＋2≤0，
等号成立条件x＝0，
∴h(x)值域(－∞，0]∪{1}∪[4，＋∞)．
方法二：y＝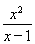
，x2－yx＋y＝0.
∵x∈R且x≠1，则关于x的方程有实根，
∴Δ＝y2－4y≥0，∴y≥4或y≤0，
∴h(x)值域(－∞，0]∪{1}∪[4，＋∞)．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
