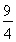Question

已知f(x)＝x3－6x2＋9x－abc，a＜b＜c，且f(a)＝f(b)＝f(c)＝0.现给出如下结论：

①f(0)f(1)＞0；②f(0)f(1)＜0；③f(0)f(3)＞0；

④f(0)f(3)＜0.

其中正确结论的序号是(　　)

A．①③ B．①④

C．②③ D．②④

 

Answer 1

C

【解析】∵f(x)＝x3－6x2＋9x－abc.

∴f′(x)＝3x2－12x＋9＝3(x－1)(x－3)，

令f′(x)＝0，得x＝1或x＝3.

依题意有，函数f(x)＝x3－6x2＋9x－abc的图象与x轴有三个不同的交点，故f(1)f(3)＜0，

即(1－6＋9－abc)(33－6×32＋9×3－abc)＜0，

∴0＜abc＜4，∴f(0)＝－abc＜0，f(1)＝4－abc＞0，f(3)＝－abc＜0，故②③是对的，应选C.