题目内容
14.已知sinα-sinβ=$\frac{1}{3}$,cosα+cosβ=$\frac{3}{7}$,0<α,β<$\frac{π}{2}$,求sin$\frac{α+β}{2}$的值.分析 将已知等式两边平方后相加,由二倍角的余弦函数公式即可得解.
解答 解:∵sinα-sinβ=$\frac{1}{3}$,两边平方可得:sin2α+sin2β-2sinαsinβ=$\frac{1}{9}$,①
cosα+cosβ=$\frac{3}{7}$,两边平方可得:cos2α+cos2β+2cosαcosβ=$\frac{9}{49}$,②
∴①+②可得:2+2cos(α+β)=$\frac{130}{441}$,可解得:cos(α+β)=-$\frac{377}{441}$=1-sin2$\frac{α+β}{2}$,
∴可得:sin2$\frac{α+β}{2}$=$\frac{818}{441}$,
∵0<α,β<$\frac{π}{2}$,∴0<$\frac{α+β}{2}$<$\frac{π}{2}$,
∴sin$\frac{α+β}{2}$=$\sqrt{\frac{818}{441}}$.
点评 本题主要考查了二倍角的正弦公式的应用,注意讨论角的范围,计算量比较大,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
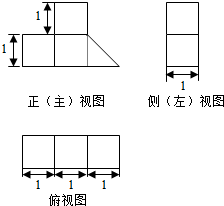

| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
4.已知函数y=f(x)的定义域是[0,2],那么g(x)=$\frac{f({x}^{2})}{1+lg(x+1)}$的定义域是( )
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
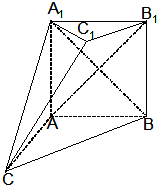 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1