题目内容
【题目】在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC= ![]() ,AB=2BC=2,且AC⊥FB.
,AB=2BC=2,且AC⊥FB. 
(1)求证:平面EAC⊥平面FCB;
(2)若线段AC上存在点M,使AE∥平面FDM,求 ![]() 的值.
的值.
【答案】
(1)证明:在△ABC中,
∵AC= ![]() ,AB=2BC=2,
,AB=2BC=2,
∴AC2+BC2=AB2.
∴AC⊥BC.
又∵AC⊥FB,BF∩CB=B,
∴AC⊥平面FBC.
∵AC平面平面EAC,
∴平面EAC⊥平面FCB.
(2)解:线段AC上存在点M,且M为AC中点时,有EA∥平面FDM,
证明如下:
连接CE与DF交于点N,连接MN.
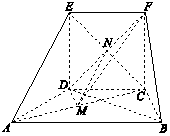
由 CDEF为正方形,得N为CE中点.
∴EA∥MN.
∵MN平面FDM,EA平面FDM,
∴EA∥平面FDM.
所以线段AC上存在点M,且 ![]() =1,使得EA∥平面FDM成立.
=1,使得EA∥平面FDM成立.
【解析】(1)推导出AC⊥BC,AC⊥FB,从而AC⊥平面FBC,由上能证明平面EAC⊥平面FCB.(2)线段AC上存在点M,且M为AC中点时,连接CE与DF交于点N,连接MN.则EA∥MN.由此推导出线段AC上存在点M,且 ![]() =1,使得EA∥平面FDM成立.
=1,使得EA∥平面FDM成立.
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

练习册系列答案
相关题目