题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知AA1=AB=AC,BC= ![]() AB,且AA1⊥平面ABC,点M、Q分别是BC、CC1的中点,点P是棱A1B1上的任一点.
AB,且AA1⊥平面ABC,点M、Q分别是BC、CC1的中点,点P是棱A1B1上的任一点. 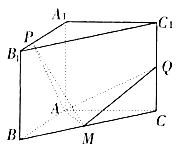
(1)求证:AQ⊥MP;
(2)若平面ACC1A1与平面AMP所成的锐角二面角为θ,且cosθ= ![]() ,试确定点P在棱A1B1上的位置,并说明理由.
,试确定点P在棱A1B1上的位置,并说明理由.
【答案】
(1)证明:∵在三棱柱ABC﹣A1B1C1中,AA1=AB=AC,BC= ![]() AB,
AB,
∴由已知得AB2+AC2=BC2,∴AB⊥AC,
又AA1⊥平面ABC,∴AA1,AB,AC两两垂直,
如图,
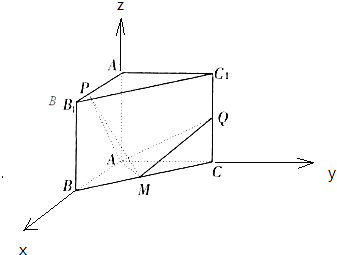
以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,
设AB=1,则A(0,0,0),C(0,1,0),B(1,0,0),M( ![]() ,
, ![]() ,0),Q(0,1,
,0),Q(0,1, ![]() ),
),
设P(x0,0,1),(0≤x0≤1),
![]() =(0,1,
=(0,1, ![]() ),
), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,1),
,1),
∵ ![]() =0﹣
=0﹣ ![]() +
+ ![]() =0,∴
=0,∴ ![]() ⊥
⊥ ![]() ,
,
∴AQ⊥MP
(2)解:由已知得AB⊥平面ACC1A1,
∴平面ACC1A1的一个法向量为 ![]() =(1,0,0),
=(1,0,0),
![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(x0,0,1),
=(x0,0,1),
设平面AMP的一个法向量 ![]() =(x,y,z),
=(x,y,z),
则 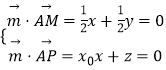 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,﹣x0),
=(1,﹣1,﹣x0),
∵平面ACC1A1与平面AMP所成的锐角二面角为θ,且cosθ= ![]() ,
,
∴cosθ=|cos< ![]() >|=
>|= ![]() =
= ![]() =
= ![]() ,
,
解得x0= ![]() ,
,
∴P( ![]() ,0,1),∴P是棱A1B1的中点.
,0,1),∴P是棱A1B1的中点.
【解析】(1)由勾股定理得AB⊥AC,以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能证明AQ⊥MP.(2)求出平面ACC1A1的一个法向量和平面AMP的一个法向量,利用向量法能求出P( ![]() ,0,1),P是棱A1B1的中点.
,0,1),P是棱A1B1的中点.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x | | | |||
f(x) | 0 | 3 | 0 | ﹣3 | 0 |
(1)请将表中数据补充完整,并直接写出函数f(x)的解析式;
(2)若将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,求当x∈[﹣ ![]() ,
, ![]() ]时,函数g(x)的值域;
]时,函数g(x)的值域;
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若=h(x)图象的一个对称中心为( ![]() ),求θ的最小值.
),求θ的最小值.
