Question

【题目】某地政府落实党中央“精准扶贫”政策，解决一贫困山村的人畜用水困难，拟修建一个底面为正方形（由地形限制边长不超过10m）的无盖长方体蓄水池，设计蓄水量为800m3 ． 已知底面造价为160元/m2 ， 侧面造价为100元/m2 ． （I）将蓄水池总造价f（x）（单位：元）表示为底面边长x（单位：m）的函数；
（II）运用函数的单调性定义及相关知识，求蓄水池总造价f（x）的最小值．

Answer 1

【答案】解：（Ⅰ）设蓄水池高为h，则 ，

∴

=

（Ⅱ）任取x1，x2∈（0，10]，且x1＜x2，则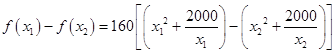

=

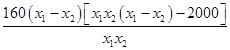
∵0＜x1＜x2≤10，∴x1x2＞0，x1﹣x2＜0，x1x2（x1+x2）＜2000，

∴y=f（x1）﹣f（x2），即f（x1）＞f（x2），∴y=f（x）在x∈（0，10]上单调递减

故x=10当时，fmin（x）=f（10）=48000

答：当底面边长为10m时，蓄水池最低造价为48000元

【解析】（I）设蓄水池高为h，则 ，利用底面造价为160元/m2，侧面造价为100元/m2，即可将蓄水池总造价f（x）（单位：元）表示为底面边长x（单位：m）的函数；（II）确定y=f（x）在x∈（0，10]上单调递减，即可求蓄水池总造价f（x）的最小值．
【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点，需要掌握用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”才能正确解答此题．