题目内容
【题目】已知函数![]() ae2x+(a﹣2) ex﹣x.
ae2x+(a﹣2) ex﹣x.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)讨论![]() 单调性,首先进行求导,发现式子特点后要及时进行因式分解,再对
单调性,首先进行求导,发现式子特点后要及时进行因式分解,再对![]() 按
按![]() ,
, ![]() 进行讨论,写出单调区间;(2)根据第(1)问,若
进行讨论,写出单调区间;(2)根据第(1)问,若![]() ,
, ![]() 至多有一个零点.若
至多有一个零点.若![]() ,当
,当![]() 时,
时, ![]() 取得最小值,求出最小值
取得最小值,求出最小值![]() ,根据
,根据![]() ,
, ![]() ,
, ![]() 进行讨论,可知当
进行讨论,可知当![]() 时有2个零点.易知
时有2个零点.易知![]() 在
在![]() 有一个零点;设正整数
有一个零点;设正整数![]() 满足
满足![]() ,则
,则![]() .由于
.由于![]() ,因此
,因此![]() 在
在![]() 有一个零点.从而可得
有一个零点.从而可得![]() 的取值范围为
的取值范围为![]() .
.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
(ⅰ)若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递减.
单调递减.
(ⅱ)若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)(ⅰ)若![]() ,由(1)知,
,由(1)知, ![]() 至多有一个零点.
至多有一个零点.
(ⅱ)若![]() ,由(1)知,当
,由(1)知,当![]() 时,
时, ![]() 取得最小值,最小值为
取得最小值,最小值为![]() .
.
①当![]() 时,由于
时,由于![]() ,故
,故![]() 只有一个零点;
只有一个零点;
②当![]() 时,由于
时,由于![]() ,即
,即![]() ,故
,故![]() 没有零点;
没有零点;
③当![]() 时,
时, ![]() ,即
,即![]() .
.
又![]() ,故
,故![]() 在
在![]() 有一个零点.
有一个零点.
设正整数![]() 满足
满足![]() ,则
,则![]() .
.
由于![]() ,因此
,因此![]() 在
在![]() 有一个零点.
有一个零点.
综上, ![]() 的取值范围为
的取值范围为![]() .
.
点睛:研究函数零点问题常常与研究对应方程的实根问题相互转化.已知函数![]() 有2个零点求参数a的取值范围,第一种方法是分离参数,构造不含参数的函数,研究其单调性、极值、最值,判断
有2个零点求参数a的取值范围,第一种方法是分离参数,构造不含参数的函数,研究其单调性、极值、最值,判断![]() 与其交点的个数,从而求出a的取值范围;第二种方法是直接对含参函数进行研究,研究其单调性、极值、最值,注意点是若
与其交点的个数,从而求出a的取值范围;第二种方法是直接对含参函数进行研究,研究其单调性、极值、最值,注意点是若![]() 有2个零点,且函数先减后增,则只需其最小值小于0,且后面还需验证最小值两边存在大于0的点.
有2个零点,且函数先减后增,则只需其最小值小于0,且后面还需验证最小值两边存在大于0的点.

【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某个餐厅打算从上表的6种等级的中国小龙虾中随机选2种进行促销,记被选中的2种等级代码数值在60以下(不含60)的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:对一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: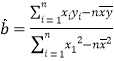 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.