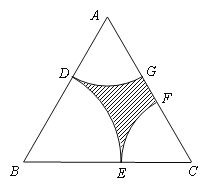
题目内容
【题目】在平面直角坐标系中，已知圆心
在直线
上的圆
经过点
，但不经过坐标原点，并且直线
与圆
相交所得的弦长为4.
（1）求圆
的一般方程；
（2）若从点
发出的光线经过
轴反射，反射光线刚好通过圆
的圆心，求反射光线所在的直线方程（用一般式表达）.
【答案】（1）
；（2）反射光线所在的直线方程的一般式为： 
.
【解析】试题分析：（1）设圆
，根据圆心
在直线
上，圆
经过点
，并且直线
与圆
相交所得的弦长为
，列出关于
的方程组，解出
的值，可得圆的标准方程，再化为一般方程即可；（2）点
关于
轴的对称点
，反射光线所在的直线即为
，又因为
，
利用两点式可得反射光线所在的直线方程，再化为一般式即可.
试题解析：（1）设圆
，
因为圆心
在直线
上，所以有： 
，
又因为圆
经过点
，所以有： 
，
而圆心到直线
的距离为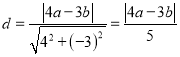
，
由弦长为4，我们有弦心距
.
所以有
联立成方程组解得：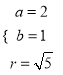 
或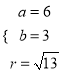
，
又因为
通过了坐标原点，所以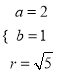
舍去.
所以所求圆的方程为： 
，
化为一般方程为： 
.
（2）点
关于
轴的对称点
，
反射光线所在的直线即为
，又因为
，
所以反射光线所在的直线方程为： 
，
所以反射光线所在的直线方程的一般式为： 
.
练习册系列答案
名校课堂系列答案
相关题目
