题目内容
【题目】如图所示,三国时代数学家赵爽在《周髀算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一内角为![]() ,若向弦图内随机抛掷500颗米粒(大小忽略不计,取
,若向弦图内随机抛掷500颗米粒(大小忽略不计,取![]() ),则落在小正方形(阴影)内的米粒数大约为( )
),则落在小正方形(阴影)内的米粒数大约为( )
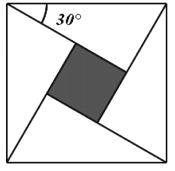
A. 134 B. 67 C. 200 D. 250
【答案】B
【解析】
设大正方形的边长为2x,则小正方形的边长为![]() x,由此利用几何概型概率计算公式能求出向弦图内随机抛掷500颗米粒(大小忽略不计),落在小正方形(阴影)内的米粒数个数.
x,由此利用几何概型概率计算公式能求出向弦图内随机抛掷500颗米粒(大小忽略不计),落在小正方形(阴影)内的米粒数个数.
设大正方形的边长为2x,则小正方形的边长为![]() x,
x,
向弦图内随机抛掷500颗米粒(大小忽略不计),
设落在小正方形(阴影)内的米粒数大约为a,
则![]() ,
,
解得a=500(![]() )≈67.
)≈67.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值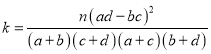
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?