题目内容
13.已知甲乙两个商场相距6公里,由于交通的原因市民到甲商场每公里车费到乙商场每公里车费的2倍,若甲乙两个商场同种商品价格都相同,为了节约起见,试确定市民到甲乙两个商场购物的地区分界线,并画出到甲商场购物的市民分布地区图.分析 以甲乙两商场的中点为原点,以甲乙两商场所在直线为x轴,建立如图的直角坐标系,求得甲乙的坐标,设出分界线上的点的坐标为(x,y),由题意,可得到甲乙两商场的路程之比为1:2,由两点的距离公式,化简整理,即可得到所求点的轨迹方程及轨迹,进而得到所求区域.
解答 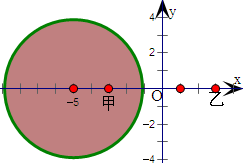 解:以甲乙两商场的中点为原点,
解:以甲乙两商场的中点为原点,
以甲乙两商场所在直线为x轴,建立如图的直角坐标系,
即有甲商场的坐标为(-3,0),乙商场的坐标为(3,0),
设市民到甲乙两个商场购物的地区分界线上
的点的坐标为(x,y),
由市民到甲商场每公里车费到乙商场每公里车费的2倍,
可得到甲乙两商场的路程之比为1:2,
即有$\frac{\sqrt{(x+3)^{2}+{y}^{2}}}{\sqrt{(x-3)^{2}+{y}^{2}}}$=$\frac{1}{2}$,
两边平方,化简可得,
x2+y2+10x+9=0,
即为(x+5)2+y2=16,
故市民到甲乙两个商场购物的地区分界线为(-5,0)为圆心,4为半径的圆,
到甲商场购物的市民分布地区图为圆及内部的区域.
点评 本题考查直线和圆的应用题,考查圆的方程的求法,考查运算能力,属于中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
8.不等式x+2y-1>0表示直线x+2y-1=0( )
| A. | 上方的平面区域 | B. | 下方的平面区域 | ||
| C. | 上方的平面区域(包括直线) | D. | 下方的平面区域(包括直线) |