题目内容
曲线f(x)= ex-f(0)x+
ex-f(0)x+ x2在点(1,f(1))处的切线方程为________.
x2在点(1,f(1))处的切线方程为________.
 ex-f(0)x+
ex-f(0)x+ x2在点(1,f(1))处的切线方程为________.
x2在点(1,f(1))处的切线方程为________.y=ex-

由已知得f(0)= ,
,
∴f(x)= ex-
ex- x+
x+ x2,
x2,
∴f′(x)= ex-
ex- +x,
+x,
∴f′(1)= e-
e- +1,即f′(1)=e,
+1,即f′(1)=e,
从而f(x)=ex-x+ x2,f′(x)=ex-1+x,
x2,f′(x)=ex-1+x,
∴f(1)=e- ,f′(1)=e,
,f′(1)=e,
故切线方程为y-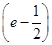 =e(x-1),即y=ex-
=e(x-1),即y=ex- .
.
 ,
,∴f(x)=
 ex-
ex- x+
x+ x2,
x2,∴f′(x)=
 ex-
ex- +x,
+x,∴f′(1)=
 e-
e- +1,即f′(1)=e,
+1,即f′(1)=e,从而f(x)=ex-x+
 x2,f′(x)=ex-1+x,
x2,f′(x)=ex-1+x,∴f(1)=e-
 ,f′(1)=e,
,f′(1)=e,故切线方程为y-
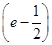 =e(x-1),即y=ex-
=e(x-1),即y=ex- .
.
练习册系列答案
相关题目
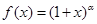 的定义域是
的定义域是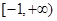 ,其中常数
,其中常数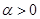 .
.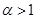 ,求
,求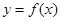 的过原点的切线方程.
的过原点的切线方程.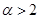 时,求最大实数
时,求最大实数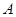 ,使不等式
,使不等式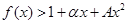 对
对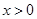 恒成立.
恒成立.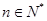 ,有
,有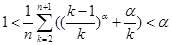 .
.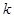 和
和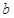 ,使得函数
,使得函数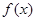 和
和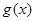 对其定义域上的任意实数
对其定义域上的任意实数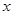 分别满足:
分别满足: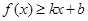 和
和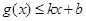 ,则称直线
,则称直线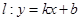 为
为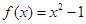 和函数
和函数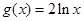 ,那么函数
,那么函数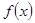 的图像如图所示,则关于
的图像如图所示,则关于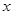 的不等式
的不等式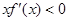 的解集为( )
的解集为( )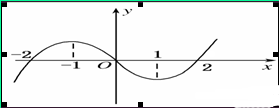
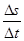 ;
;