题目内容
设函数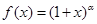 的定义域是
的定义域是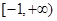 ,其中常数
,其中常数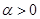 .
.
(1)若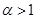 ,求
,求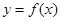 的过原点的切线方程.
的过原点的切线方程.
(2)当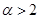 时,求最大实数
时,求最大实数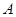 ,使不等式
,使不等式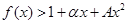 对
对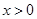 恒成立.
恒成立.
(3)证明当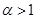 时,对任何
时,对任何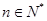 ,有
,有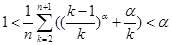 .
.
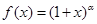 的定义域是
的定义域是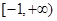 ,其中常数
,其中常数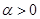 .
.(1)若
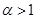 ,求
,求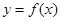 的过原点的切线方程.
的过原点的切线方程.(2)当
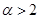 时,求最大实数
时,求最大实数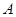 ,使不等式
,使不等式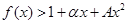 对
对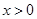 恒成立.
恒成立.(3)证明当
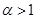 时,对任何
时,对任何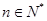 ,有
,有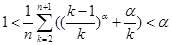 .
.(1)切线方程为 和
和 .(2)
.(2)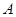 的最大值是
的最大值是 .(3)详见解析.
.(3)详见解析.
 和
和 .(2)
.(2)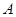 的最大值是
的最大值是 .(3)详见解析.
.(3)详见解析.试题分析:(1)一般地,曲线
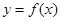 在点
在点 处的切线方程为:
处的切线方程为: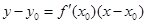 .注意,此题是求过原点的切线,而不是求
.注意,此题是求过原点的切线,而不是求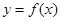 在原点处切线方程,而该曲线又过原点,故有原点为切点和原点不为切点两种情况.当原点不为切点时需把切点的坐标设出来.(2)令
在原点处切线方程,而该曲线又过原点,故有原点为切点和原点不为切点两种情况.当原点不为切点时需把切点的坐标设出来.(2)令 ,则问题转化为
,则问题转化为 对
对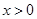 恒成立.注意到
恒成立.注意到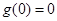 ,所以如果
,所以如果 在
在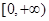 单调增,则必有
单调增,则必有 对
对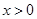 恒成立.下面就通过导数研究
恒成立.下面就通过导数研究 的单调性.(3)不等式
的单调性.(3)不等式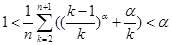 可变形为:
可变形为: .为了证这个不等式,首先证
.为了证这个不等式,首先证 ;而证这个不等式可利用导数证明
;而证这个不等式可利用导数证明 .故令
.故令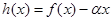 ,然后利用导数求
,然后利用导数求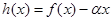 在区间
在区间 上范围即可.
上范围即可.试题解析:(1)
 .若切点为原点,由
.若切点为原点,由 知切线方程为
知切线方程为 ;
;若切点不是原点,设切点为
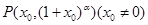 ,由于
,由于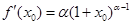 ,故由切线过原点知
,故由切线过原点知 ,在
,在 内有唯一的根
内有唯一的根 .
.又
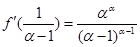 ,故切线方程为
,故切线方程为 .
.综上所述,所求切线有两条,方程分别为
 和
和 .
.(2)令
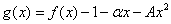 ,则
,则 ,
, ,显然有
,显然有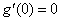 ,且
,且 的导函数为:
的导函数为: .
.若
 ,则
,则 ,由
,由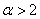 知
知 对
对 恒成立,从而对
恒成立,从而对 恒有
恒有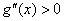 ,即
,即 在
在 单调增,从而
单调增,从而 对
对 恒成立,从而
恒成立,从而 在
在 单调增,
单调增, 对
对 恒成立.
恒成立.若
 ,则
,则 ,由
,由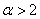 知存在
知存在 ,使得
,使得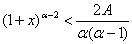 对
对 恒成立,即
恒成立,即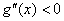 对
对 恒成立,再由
恒成立,再由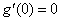 知存在
知存在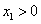 ,使得
,使得 对
对 恒成立,再由
恒成立,再由 便知
便知 不能对
不能对 恒成立.
恒成立.综上所述,所求
 的最大值是
的最大值是 .
.(3)当
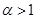 时,令
时,令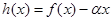 ,则
,则 ,故当
,故当 时,恒有
时,恒有 ,即
,即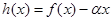 在
在 单调递减,故
单调递减,故 ,对
,对 恒成立.又
恒成立.又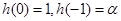 ,故
,故 ,即对
,即对 恒有:
恒有: ,
,在此不等式中依次取
 ,得:
,得: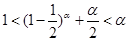 ,,
,, ,
,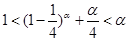 ,
, ,
,…………………………
 ,
,将以上不等式相加得:
 ,即
,即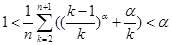 .
.
练习册系列答案
相关题目
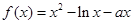 ,
,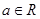 .
. 时,求
时,求 的最小值;
的最小值; ,求a的取值范围.
,求a的取值范围. 的取值范围.
的取值范围. 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为 ,则
,则 的乘积的值为( )
的乘积的值为( )


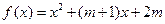 是偶函数,且
是偶函数,且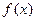 在
在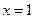 处的切线方程为
处的切线方程为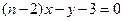 ,则常数
,则常数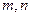 的积等于( )
的积等于( ) 在点
在点 处的切线与两坐标轴围成三角形的面积为
处的切线与两坐标轴围成三角形的面积为 ,则
,则 ________.
________.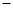 y+1=0,则( )
y+1=0,则( )  ex-f(0)x+
ex-f(0)x+ x2在点(1,f(1))处的切线方程为________.
x2在点(1,f(1))处的切线方程为________.