Question

【题目】选修4-4：坐标系与参数方程

已知曲线在平面直角坐标系下的参数方程为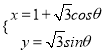（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系．

（1）求曲线的普通方程及极坐标方程；

（2）直线的极坐标方程是，射线： 与曲线交于点与直线交于点，求线段的长．

Answer 1

【答案】（1）， ；（2）.

【解析】试题分析：（1）曲线C的参数方程为（为参数），消去参数化为：（x-1）2+y2=3，展开利用互化公式即可得出极坐标方程．
（2）射线OT： （）分别与曲线C，直线l的极坐标方程联立解出交点坐标即可得出．

试题解析：

(1)消去参数化为：（x-1）2+y2=3，展开为：x2+y2-2x-2=0，

化为极坐标方程：ρ2-2ρcosθ-2=0．

（2）联立，化为：ρ2-ρ-2=0，ρ＞0，解得ρ=2．

射线OT：θ=（ρ＞0）与曲线C交于A点．

联立， 解得ρ=6，

射线OT：θ=（ρ＞0）与直线l交于B，

∴线段AB的长=6-2=4．