题目内容
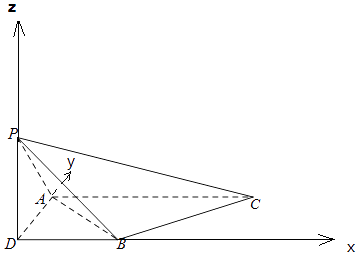
【题目】如图，三棱锥P﹣ABC，侧棱PA=2，底面三角形ABC为正三角形，边长为2，顶点P在平面ABC上的射影为D，有AD⊥DB，且DB=1．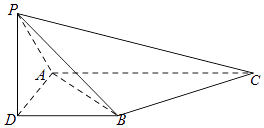 
（Ⅰ）求证：AC∥平面PDB；
（Ⅱ）求二面角P﹣AB﹣C的余弦值；
（Ⅲ）线段PC上是否存在点E使得PC⊥平面ABE，如果存在，求 
的值；如果不存在，请说明理由．
【答案】证明：（Ⅰ）因为AD⊥DB，且DB=1，
AB=2，所以 
，
所以∠DBA=60°．
因为△ABC为正三角形，所以∠CAB=60°，
又由已知可知ACBD为平面四边形，所以DB∥AC．
因为AC平面PDB，DB平面PDB，
所以AC∥平面PDB．
解：（Ⅱ）由点P在平面ABC上的射影为D可得PD⊥平面ACBD，
所以PD⊥DA，PD⊥DB．
如图，以D为原点，DB为x轴，DA为y轴，DP为z轴，建立空间直角坐标系，
则由已知可知B（1，0，0）， 
，P（0，0，1）， 
．
平面ABC的法向量 
=（0，0，1），
设 
=（x，y，z）为平面PAB的一个法向量，则
由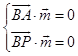 
，得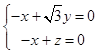 
，令y=1，则 
，所以平面PAB的一个法向量 =（ 
），
所以cos＜ 
＞= 
= 
，
由图象知二面角P﹣AB﹣C是钝二面角，所以二面角P﹣AB﹣C的余弦值为 
．
（Ⅲ）由（Ⅱ）可得 
， 
，
因为 
，
所以PC与AB不垂直，
所以在线段PC上不存在点E使得PC⊥平面ABE．
【解析】（Ⅰ）推导出∠DBA=∠CAB=60°，ACBD为平面四边形，从而DB∥AC．由此能证明AC∥平面PDB．（Ⅱ）由点P在平面ABC上的射影为D可得PD⊥平面ACBD，以D为原点，DB为x轴，DA为y轴，DP为z轴，建立空间直角坐标系，利用向量法能求出二面角P﹣AB﹣C的余弦值．（Ⅲ）求出 
， 
，由 
≠0，求出在线段PC上不存在点E使得PC⊥平面ABE．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
