题目内容
设 与
与 是定义在同一区间[a,b]上的两个函数,若对任意
是定义在同一区间[a,b]上的两个函数,若对任意 ∈[a,b],都有
∈[a,b],都有 成立,则称
成立,则称 和
和 在[a,b]上是“亲密函数”,区间[a,b]称为“亲密区间”.若
在[a,b]上是“亲密函数”,区间[a,b]称为“亲密区间”.若 与
与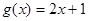 在[a,b]上是“亲密函数”,则其“亲密区间”可以是
在[a,b]上是“亲密函数”,则其“亲密区间”可以是
 与
与 是定义在同一区间[a,b]上的两个函数,若对任意
是定义在同一区间[a,b]上的两个函数,若对任意 ∈[a,b],都有
∈[a,b],都有 成立,则称
成立,则称 和
和 在[a,b]上是“亲密函数”,区间[a,b]称为“亲密区间”.若
在[a,b]上是“亲密函数”,区间[a,b]称为“亲密区间”.若 与
与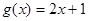 在[a,b]上是“亲密函数”,则其“亲密区间”可以是
在[a,b]上是“亲密函数”,则其“亲密区间”可以是 | A.[0,2] | B.[0,1] | C.[1,2] | D.[-1,0] |
B
根据“亲密函数”的定义列出绝对值不等式|x2+x+2-(2x+1)|≤1,求出解集即可得到它的“亲密区间”.
解:因为f(x)与g(x)在[a,b]上是“亲密函数”,
则|f(x)-g(x)|≤1即|x2+x+2-(2x+1)|≤1即|x2-x+1|≤1,
化简得-1≤x2-x+1≤1,因为x2-x+1的△<0即与x轴没有交点,由开口向上得到x2-x+1>0>-1恒成立;
所以由x2-x+1≤1解得0≤x≤1,所以它的“亲密区间”是[0,1]
故选B
解:因为f(x)与g(x)在[a,b]上是“亲密函数”,
则|f(x)-g(x)|≤1即|x2+x+2-(2x+1)|≤1即|x2-x+1|≤1,
化简得-1≤x2-x+1≤1,因为x2-x+1的△<0即与x轴没有交点,由开口向上得到x2-x+1>0>-1恒成立;
所以由x2-x+1≤1解得0≤x≤1,所以它的“亲密区间”是[0,1]
故选B

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 ,其中常数
,其中常数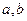 满足
满足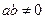 。
。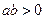 ,判断函数
,判断函数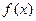 的单调性;
的单调性;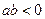 ,求
,求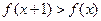 时
时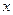 折取值范围。
折取值范围。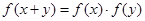 ,且
,且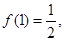 则
则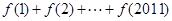 = ( )
= ( )



 ,一元二次方程
,一元二次方程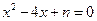 有整数根的冲要条件是
有整数根的冲要条件是
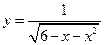 的定义域是 .
的定义域是 . 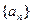 的通项公式
的通项公式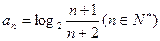 ,设
,设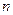 项和为
项和为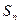 ,则使
,则使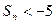 成立的自然数
成立的自然数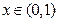 时,
时,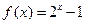 ,则
,则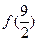 = .
= . =
= ,则不等式
,则不等式 的解集为 .
的解集为 .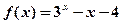 的一个零点,其参考如下数据:
的一个零点,其参考如下数据:
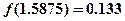




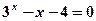 的一个近似解(精确到
的一个近似解(精确到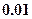 )为
)为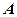 .
. 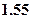

 .
. 
 .
. 
 .
. 