题目内容
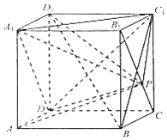
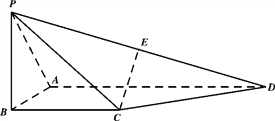
【题目】如图所示,在四棱锥![]() 中,平面
中,平面![]() ⊥平面
⊥平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求证: ![]() ⊥
⊥![]() ;
;
(Ⅲ)若点![]() 在棱
在棱![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3) ![]() .
.
【解析】试题分析:(1)证明线线平行: ![]() ⊥
⊥![]() ,再由面面平行的性质得到
,再由面面平行的性质得到![]() ⊥平面
⊥平面![]() ;(2)先证得
;(2)先证得![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,故得到
,故得到![]() ⊥平面
⊥平面![]() ,所以
,所以![]() ⊥
⊥![]() ;(3)根据题意做出辅助线并证明四边形
;(3)根据题意做出辅助线并证明四边形![]() 为平行四边形,由平行线分线段成比例得到
为平行四边形,由平行线分线段成比例得到![]() .
.
解析:
(Ⅰ)证明:因为![]() ,所以
,所以![]() ⊥
⊥![]() .
.
因为平面![]() ⊥平面
⊥平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() ⊥平面
⊥平面![]() .
.
(Ⅱ)证明:由已知得![]() ⊥
⊥![]()
因为![]() ,
,
所以![]() ⊥
⊥![]() .
.
又因为![]() ,
,
所以![]() ⊥
⊥![]() .
.
因为![]()
所以![]() ⊥平面
⊥平面![]()
所以![]() ⊥
⊥![]() .
.
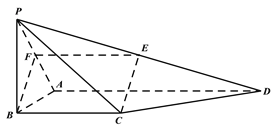
(Ⅲ)解:过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
因为![]() ,
,
所以![]() .
.
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点共面.
四点共面.
又因为![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,
,
且平面![]()
![]() 平面
平面![]() ,
,
所以![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() .
.
在△![]() 中,因为
中,因为![]() ,
,
所以![]() ,
,
即![]() .
.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】已知直线![]() .
.
(1)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,求
,求![]() 的面积的最小值并求此时直线
的面积的最小值并求此时直线![]() 的方程;
的方程;
(3)已知点![]() ,若点
,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值并求此时直线
的最大值并求此时直线![]() 的方程.
的方程.
【题目】流行性感冒多由病毒引起,据调查,空气月平均相对湿度过大或过小时,都有利于一些病毒繁殖和传播,科学测定,当空气月平均相对湿度大于65010或小于![]() 时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度.
时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度.
第一季度 | 第二季度 | 第三季度 | 第四季度 | |||||||||
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
甲地 |
|
|
|
|
|
|
|
|
|
|
| |
乙地 |
|
|
|
|
|
|
|
|
|
|
|
|
(I)从上表12个月中,随机取出1个月,求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率;
(Ⅱ)从上表第一季度和第二季度的6个月中随机取出2个月,记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)若![]() ,设乙地上表12个月的空气月平均相对湿度的中位数为
,设乙地上表12个月的空气月平均相对湿度的中位数为![]() ,求
,求![]() 的最大值和最小值.(只需写出结论)
的最大值和最小值.(只需写出结论)
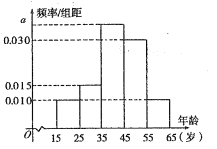
【题目】某班同学利用国庆节进行社会实践,对![]() 的人群随机抽取
的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳组的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
(1)补全频率分布直方图,并求![]() ,
,![]() ,
,![]() 的值;
的值;

(2)求年龄段人数的中位数和众数;
(3)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在
岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在![]() 岁的概率.
岁的概率.