题目内容
【题目】已知直线![]() .
.
(1)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,求
,求![]() 的面积的最小值并求此时直线
的面积的最小值并求此时直线![]() 的方程;
的方程;
(3)已知点![]() ,若点
,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值并求此时直线
的最大值并求此时直线![]() 的方程.
的方程.
【答案】(1)[0,+∞);(2)S的最小值为4,此时的直线方程为x2y+4=0;(3)d的最大值为5,此时直线方程为3x+4y+2=0。
【解析】
(1)把已知方程变形,利用线性方程求出直线所过定点即可;化直线方程为斜截式,由斜率大于等于0且在y轴上的截距大于等于0联立不等式组求解;
(2)由题意画出图形,求出直线在两坐标轴上的截距,代入三角形面积公式,利用基本不等式求最值;
(3)当PM⊥l时,d取得最大值,由两点的距离公式可得最大值,求得PM的斜率,可得直线l的斜率,由点斜式方程可得所求直线l的方程.
(1)由kxy+1+2k=0,得k(x+2)+(y+1)=0,
联立![]() ,解得
,解得![]() ,
,
则直线l:kxy+1+2k=0过定点M(2,1);
由kxy+1+2k=0,得y=kx+1+2k,
要使直线不经过第四象限,则![]() ,解得k0。
,解得k0。
∴k的取值范围是[0,+∞)。
(2)如图,
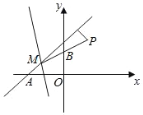
由题意可知,k>0,
在kxy+1+2k=0中,取y=0,得![]() ,取x=0,得y=1+2k,
,取x=0,得y=1+2k,
∴![]()
![]() 。
。
当且仅当![]() ,即
,即![]() 时等号成立。
时等号成立。
∴S的最小值为4,此时的直线方程为12xy+2=0,即x2y+4=0。
(3)点P(1,5),若点P到直线l的距离为d,
当PM⊥l时,d取得最大值,且为![]() ,
,
由直线PM的斜率为![]() ,
,
可得直线直线l的斜率为![]() ,
,
则直线l的方程为![]() ,
,
即为3x+4y+2=0。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目