题目内容
17.已知函数f(x)=$lo{g}_{\frac{1}{3}}$$\frac{ax-6}{x-2}$(a为常数)在区间(3,5)上是减函数,求实数a的取值范围.分析 设t=$\frac{ax-6}{x-2}$,利用复合函数单调性之间的关系进行求解即可.
解答 解:设t=g(x)=$\frac{ax-6}{x-2}$,则函数y=log${\;}_{\frac{1}{3}}$t为减函数,
∵f(x)=$lo{g}_{\frac{1}{3}}$$\frac{ax-6}{x-2}$(a为常数)在区间(3,5)上是减函数,
∴函数t=g(x)=$\frac{ax-6}{x-2}$在区间(3,5)上是增函数,且g(3)≥0
t=g(x)=$\frac{ax-6}{x-2}$=$\frac{a(x-2)+2a-6}{x-2}$=a+$\frac{2a-6}{x-2}$,
若t=g(x)=$\frac{ax-6}{x-2}$在区间(3,5)上是增函数,则2a-6<0,即a<3,
由g(3)≥0得g(3)=3a-6≥0,解得a≥2,
综上2≤a<3,
即实数a的取值范围是[2,3).
点评 本题主要考查函数单调性的应用,利用换元法结合对数函数和分数函数的单调性是解决本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.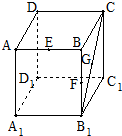 有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )
 有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{47}{48}$ |
12.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+2$\overrightarrow{b}$|=4$\sqrt{2}$,则$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是( )
| A. | (-∞,4] | B. | [4,+∞) | C. | (-∞,2] | D. | [2,+∞) |
9.已知集合A={0,1,x2-5x},有-4∈A,则实数x的值为( )
| A. | 1 | B. | 4 | C. | 1或4 | D. | 36 |
7.已知α为第二象限角,sinα=$\frac{4}{5}$,则sin(π-2α)=( )
| A. | -$\frac{24}{25}$ | B. | $\frac{24}{25}$ | C. | $\frac{12}{25}$ | D. | -$\frac{12}{25}$ |