题目内容
8.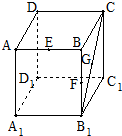 有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1,在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{47}{48}$ |
分析 根据正方体的几何特征,我们选取过E,B1,G三点的平面去截正方体,根据棱锥的体积公式,易求出切下的小三棱锥的体积,进而求出剩下的即容器可装水的容积,进而得到答案.
解答 解:以E,B1,G三点组成的平面去截正方体
截去一个三棱锥
其底面为△EBB1,面积S=$\frac{1}{2}$a×1×$\frac{1}{2}$=$\frac{1}{4}$
高为h=1
截去一个三棱锥体积为V=$\frac{1}{3}$S•h=$\frac{1}{3}$•$\frac{1}{4}$•1=$\frac{1}{12}$
当E,B1,G三点在同一水平面时,F点在水平面之上
E,F,G三点都不漏水
其可装水最大容积1-$\frac{1}{12}$=$\frac{11}{12}$
故选C.
点评 本题考查的知识点是棱锥的体积,其中根据正方体的几何特征确定出选取过E,B1,G三点的平面去截正方体时,该容器可装水的容积最大是解答本题的关键,本题易将该容器可装水的容积最大时的情况错理解过水面过EFG三点,而错解为B.

练习册系列答案
相关题目
17.已知函数f(x+1)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式(x1-x2)[f(x1)-f(x2)]>0恒成立,则不等式f(1-x)<0的解集为( )
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
16.已知Sn是等差数列{an}的前n项和,若a2015=S2015=2015,则首项a1=( )
| A. | 2015 | B. | -2015 | C. | 2013 | D. | -2013 |
3.在△ABC中,sinA;sinB:sinC=2:3:4,则cosA:cosB:cosC=( )
| A. | 2:3:4 | B. | 14:11:(-4) | C. | 4:3:2 | D. | 7:11:(-2) |