题目内容
7.已知函数f(x)=lnx-$\frac{a(x-1)}{x+1}$.(Ⅰ)若函数f(x)在(0,+∞)上为单调增函数,求a的取值范围;
(Ⅱ)设m>n>0,求证:$\frac{m-n}{lnm-lnn}<\frac{m+n}{2}$.
分析 (Ⅰ)先求出函数f(x)的导数,通过函数的单调性得2a-2≤x+$\frac{1}{x}$,设g(x)=x+$\frac{1}{x}$,求出g(x)的最小值即可;
(Ⅱ)问题转化为只需证ln$\frac{m}{n}$-$\frac{2(\frac{m}{n}-1)}{\frac{m}{n}+1}$>0,设h(x)=lnx-$\frac{2(x-1)}{x+1}$,通过函数的单调性得到h(x)>0即可.
解答 (Ⅰ)解:f′(x)=$\frac{1}{x}$-$\frac{a(x+1)-a(x-1)}{{(x+1)}^{2}}$=$\frac{{x}^{2}+(2-2a)x+1}{{x(x+1)}^{2}}$,
因为f(x)在(0,+∞)上为单调增函数,
所以f′(x)>0在(0,+∞)上恒成立,
即x2+(2-2a)x+1≥0在(0,+∞)上恒成立.
当x∈(0,+∞)时,由x2+(2-2a)x+1≥0,
得2a-2≤x+$\frac{1}{x}$.
设g(x)=x+$\frac{1}{x}$,x∈(0,+∞),g(x)=x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
当且仅当x=$\frac{1}{x}$,即x=1时,g(x)有最小值2,
所以2a-2≤2,所以a≤2,
所以a的取值范围是(-∞,2].
(Ⅱ)证明:要证:$\frac{m-n}{lnm-lnn}<\frac{m+n}{2}$,
∵m>n>0,∴ln$\frac{m}{n}$>0,只需证$\frac{\frac{m}{n}-1}{ln\frac{m}{n}}<\frac{\frac{m}{n}+1}{2}$,
即证ln$\frac{m}{n}$>$\frac{2(\frac{m}{n}-1)}{\frac{m}{n}+1}$,只需证ln$\frac{m}{n}$-$\frac{2(\frac{m}{n}-1)}{\frac{m}{n}+1}$>0,
设h(x)=lnx-$\frac{2(x-1)}{x+1}$,
由(Ⅰ)知h(x)在(1,+∞)上是单调增函数,又$\frac{m}{n}$>1,
所以h($\frac{m}{n}$)>h(1)=0,即ln$\frac{m}{n}$-$\frac{2(\frac{m}{n}-1)}{\frac{m}{n}+1}$>0成立,
所以$\frac{m-n}{lnm-lnn}<\frac{m+n}{2}$成立.
点评 本题考查了函数的单调性、最值问题,考查函数恒成立问题,不等式的证明,是一道中档题.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
| A. | 2015 | B. | -2015 | C. | 2013 | D. | -2013 |
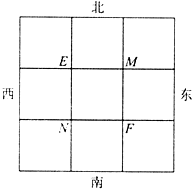 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B. 如图,是某市1000户居民月平均用电量的频率分布直方图,
如图,是某市1000户居民月平均用电量的频率分布直方图,