题目内容
如图所示,在△ABC中,AD⊥BC于D,下列条件:
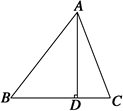
(1)∠B+∠DAC=90°;
(2)∠B=∠DAC;
(3)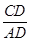 =
=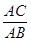 ;
;
(4)AB2=BD·BC.
其中一定能够判定△ABC是直角三角形的共有
A.3个 B.2个 C.1个 D.0个

(1)∠B+∠DAC=90°;
(2)∠B=∠DAC;
(3)
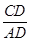 =
=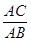 ;
;(4)AB2=BD·BC.
其中一定能够判定△ABC是直角三角形的共有
A.3个 B.2个 C.1个 D.0个
A
(1)不能判定△ABC为直角三角形,因为∠B+∠DAC=90°,而∠B+∠DAB=90°,∴∠BAD=∠DAC,∴∠B=∠C,不能判定∠BAD+∠DAC=90°;而(2)中∠B=∠DAC,∠C为公共角,∴△ABC∽△DAC,∵△DAC为直角三角形,∴△ABC为直角三角形;在(3)中,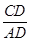 =
=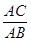 可得△ACD∽△BAD,所以∠BAD=∠C,∠B=∠DAC,∴∠BAD+∠DAC=90°;而(4)中AB2=BD·BC,即
可得△ACD∽△BAD,所以∠BAD=∠C,∠B=∠DAC,∴∠BAD+∠DAC=90°;而(4)中AB2=BD·BC,即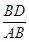 =
=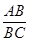 ,∠B为公共角,∴△ABC∽△DBA,即△ABC为直角三角形.
,∠B为公共角,∴△ABC∽△DBA,即△ABC为直角三角形.
∴正确命题有3个.
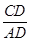 =
=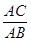 可得△ACD∽△BAD,所以∠BAD=∠C,∠B=∠DAC,∴∠BAD+∠DAC=90°;而(4)中AB2=BD·BC,即
可得△ACD∽△BAD,所以∠BAD=∠C,∠B=∠DAC,∴∠BAD+∠DAC=90°;而(4)中AB2=BD·BC,即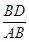 =
=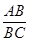 ,∠B为公共角,∴△ABC∽△DBA,即△ABC为直角三角形.
,∠B为公共角,∴△ABC∽△DBA,即△ABC为直角三角形.∴正确命题有3个.

练习册系列答案
相关题目

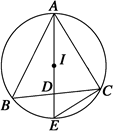
 ,连接DE交BC于点F,AC=4,BC=3.求证:
,连接DE交BC于点F,AC=4,BC=3.求证: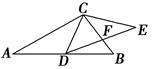
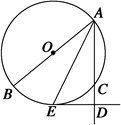
 =
= ,AE=BE,则有
,AE=BE,则有