题目内容
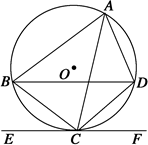
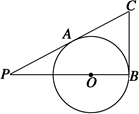
如图所示,CD为Rt△ABC斜边AB边上的中线,CE⊥CD,CE=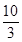 ,连接DE交BC于点F,AC=4,BC=3.求证:
,连接DE交BC于点F,AC=4,BC=3.求证:
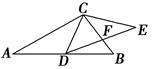
(1)△ABC∽△EDC;
(2)DF=EF.
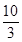 ,连接DE交BC于点F,AC=4,BC=3.求证:
,连接DE交BC于点F,AC=4,BC=3.求证:
(1)△ABC∽△EDC;
(2)DF=EF.
见解析
证明 (1)在Rt△ABC中,AC=4,BC=3,则AB=5.
∵D为斜边AB的中点,
∴AD=BD=CD=
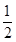 AB=2.5,
AB=2.5,∴
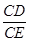 =
=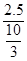 =
=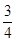 =
=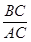 .
.∴△ABC∽△EDC,
(2)由(1)知,∠B=∠CDF,
∵BD=CD,∴∠B=∠DCF,
∴∠CDF=∠DCF.
∴DF=CF.①
由(1)知,∠A=∠CEF,∠ACD+∠DCF=90°,∠ECF+∠DCF=90°,
∴∠ACD=∠ECF.由AD=CD,得∠A=∠ACD.
∴∠ECF=∠CEF,∴CF=EF.②
由①②,知DF=EF.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

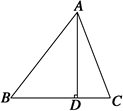
 ,点E,F分别为线段AB,AD的中点,则EF=________.
,点E,F分别为线段AB,AD的中点,则EF=________.
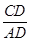 =
=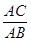 ;
;

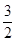 ,其中a、b分别是∠A和∠B的对边,则斜边上的高h=________.
,其中a、b分别是∠A和∠B的对边,则斜边上的高h=________.