题目内容
下列各组函数f(x)与g(x)的图象相同的是( )
A、f(x)=x,g(x)=(
| |||||
| B、f(x)=x2,g(x)=(x+1)2 | |||||
C、f(x)=|x|,g(c)=
| |||||
| D、f(x)=1,g(x)=x0 |
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:根据两个函数的定义域相同,对应关系也相同,这样的函数是相同函数,进行判断即可.
解答:
解:对于A,f(x)=x(x∈R),与g(x)=(
)2=x(x≥0)的定义域不相同,∴不是相同函数;
对于B,f(x)=x2(x∈R),与g(x)=(x+1)2(x∈R)的对应关系不相同,∴不是相同函数;
对于C,f(x)=|x|=
(x∈R),与g(x)=
(x∈R)的定义域相同,对应关系也相同,∴是相同函数;
对于D,f(x)=1(x∈R),与g(x)=x0=1(x≠0)的定义域不相同,∴不是相同函数.
故选:C.
| x |
对于B,f(x)=x2(x∈R),与g(x)=(x+1)2(x∈R)的对应关系不相同,∴不是相同函数;
对于C,f(x)=|x|=
|
|
对于D,f(x)=1(x∈R),与g(x)=x0=1(x≠0)的定义域不相同,∴不是相同函数.
故选:C.
点评:本题考查了判断函数是否为同一函数的问题,解题时应判断它们的定义域是否相同,对应关系是否也相同,是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知点M(0,2),抛物线y2=4x上的动点P到y轴的距离为d,则d+|MP|的最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
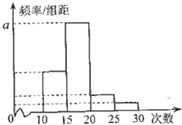 对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下: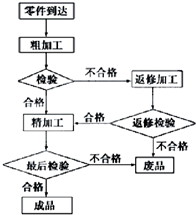 某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了
某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了