题目内容
如图所示正方体AC1,下面结论错误的是( )
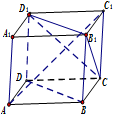

| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AD与CB1角为60° |
考点:空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:∵BD∥B1D1,BD不包含于平面CB1D1,B1D1?平面CB1D1,
∴BD∥平面CB1D1,故A正确;
∵BD⊥AC,BD⊥CC1,AC∩CC1=C,
∴BD⊥平面ACC1,
∴AC1⊥BD,故B正确;
∵BD⊥平面ACC1,BD∥B1D1,
∴AC1⊥B1D1,
设正方体AC1的棱长为1,以D为原点,建立空间直角坐标系D-xyz,
得A(1,0,0),C1(0,1,1),D1(0,0,1),C(0,1,0),
=(-1,1,1),
=(0,-1,1),
∴
•
=0-1+1=0,∴AC1⊥CD1,
∴AC1⊥平面CB1D1,故C正确;
异面直线AD与CB1角为45°,故D错误.
故选:D.
∴BD∥平面CB1D1,故A正确;
∵BD⊥AC,BD⊥CC1,AC∩CC1=C,
∴BD⊥平面ACC1,
∴AC1⊥BD,故B正确;
∵BD⊥平面ACC1,BD∥B1D1,
∴AC1⊥B1D1,
设正方体AC1的棱长为1,以D为原点,建立空间直角坐标系D-xyz,
得A(1,0,0),C1(0,1,1),D1(0,0,1),C(0,1,0),
| AC1 |
| CD1 |
∴
| AC1 |
| CD1 |
∴AC1⊥平面CB1D1,故C正确;
异面直线AD与CB1角为45°,故D错误.
故选:D.
点评:本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列变形不正确的是( )
A、由
| ||||
| B、由3x=-12,得x=-4 | ||||
C、由2x=3,得x=
| ||||
D、由
|
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.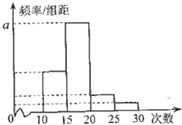 对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下: