题目内容
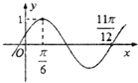 函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<
函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<| π |
| 2 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
考点:正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:首先根据函数的图象确定确定A,ω,∅的值,进一步利用函数图象的平移变换求出结果.
解答:
解:根据函数的图象:A=1,
=
-
=
则:T=π
ω=
=2
利用f(
)=1
解得:∅=kπ+
(k∈Z)
由于|∅|<
所以:∅=
求得:f(x)=sin(2x+
)
将f(x)图象上所有点的横坐标缩短来原来的
倍(纵标不变)
g(x)=sin(4x+
)
故选:A
| 3T |
| 4 |
| 11π |
| 12 |
| π |
| 6 |
| 3π |
| 4 |
则:T=π
ω=
| 2π |
| π |
利用f(
| π |
| 6 |
解得:∅=kπ+
| π |
| 6 |
由于|∅|<
| π |
| 2 |
所以:∅=
| π |
| 6 |
求得:f(x)=sin(2x+
| π |
| 6 |
将f(x)图象上所有点的横坐标缩短来原来的
| 1 |
| 2 |
g(x)=sin(4x+
| π |
| 6 |
故选:A
点评:本题考查的知识要点:利用函数的图象确定函数的解析式,主要确定A,ω,∅的值,函数图象的平移变换,属于基础题型.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
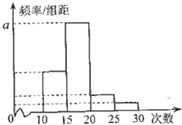 对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下: