题目内容
已知椭圆C：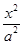
＋
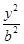＝1(a＞b＞0)的左焦点为F，C与过原点的直线相交于A，B两点，连接AF，BF.若|AB|＝10，|BF|＝8，cos∠ABF＝
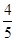，则C的离心率为________．
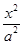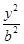＋＝1(a＞b＞0)的左焦点为F，C与过原点的直线相交于A，B两点，连接AF，BF.若|AB|＝10，|BF|＝8，cos∠ABF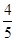＝，则C的离心率为________．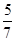
在△ABF中，由余弦定理得
|AF|2＝|AB|2＋|BF|2－2|AB|·|BF|cos∠ABF，
∴|AF|2＝100＋64－128＝36，∴|AF|＝6，
从而|AB|2＝|AF|2＋|BF|2，则AF⊥BF.
∴c＝|OF|＝
|AB|＝5，
利用椭圆的对称性，设F′为右焦点，
则|BF′|＝|AF|＝6，
∴2a＝|BF|＋|BF′|＝14，a＝7.
因此椭圆的离心率e＝
＝.
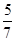|AF|2＝|AB|2＋|BF|2－2|AB|·|BF|cos∠ABF，
∴|AF|2＝100＋64－128＝36，∴|AF|＝6，
从而|AB|2＝|AF|2＋|BF|2，则AF⊥BF.
∴c＝|OF|＝
|AB|＝5，利用椭圆的对称性，设F′为右焦点，
则|BF′|＝|AF|＝6，
∴2a＝|BF|＋|BF′|＝14，a＝7.
因此椭圆的离心率e＝
＝.
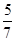练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
+
=1(a>b>0)的右焦点为F(1,0),且点(-1,
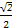)在椭圆C上.
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
·
为定值.
，且过点M
。
的直线l交椭圆C于A、B两点，且N恰好为AB中点，能否在椭圆C上找到点D，使△ABD的面积最大？若能，求出点D的坐标；若不能，请说明理由。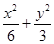
＝1，A1，A2分别为椭圆C1的左、右顶点．椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”．
的两焦点，过点F2的直线交椭圆于A，B两点．在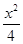
＋y2＝1的左焦点，O为坐标原点，点P在椭圆上，则
·
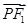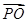的最大值为________．
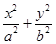＝1(a>b>0)的左、右顶点分别是A、B，左、右焦点分别是F1、F2.若|AF1|，|F1F2|，|F1B|成等比数列，则此椭圆的离心率为________．
为椭圆
的两个焦点，过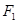
的直线交椭圆于
两点，
，则
( )
