题目内容
如图,F是椭圆的右焦点,以点F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆上的动点,P到椭圆两焦点的距离之和等于4.

(1)求椭圆和圆的标准方程;
(2)设直线l的方程为x=4,PM⊥l,垂足为M,是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

(1)求椭圆和圆的标准方程;
(2)设直线l的方程为x=4,PM⊥l,垂足为M,是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)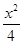 +
+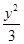 =1 (x-1)2+y2=1
=1 (x-1)2+y2=1
(2) 存在点P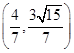 或
或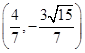 ,使得△FPM为等腰三角形
,使得△FPM为等腰三角形
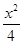 +
+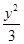 =1 (x-1)2+y2=1
=1 (x-1)2+y2=1(2) 存在点P
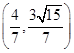 或
或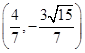 ,使得△FPM为等腰三角形
,使得△FPM为等腰三角形解:(1)由题意,设椭圆的标准方程为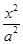 +
+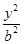 =1,由已知可得2a=4,a=2c,解得a=2,c=1,b2=a2-c2=3.
=1,由已知可得2a=4,a=2c,解得a=2,c=1,b2=a2-c2=3.
∴椭圆的标准方程为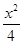 +
+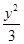 =1,圆的标准方程为(x-1)2+y2=1.
=1,圆的标准方程为(x-1)2+y2=1.
(2)设P(x,y),则M(4,y),F(1,0),-2≤x≤2,
∵P(x,y)在椭圆上,∴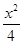 +
+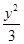 =1,
=1,
∴y2=3-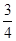 x2.
x2.
∴|PF|2=(x-1)2+y2=(x-1)2+3-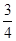 x2=
x2=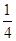 (x-4)2,
(x-4)2,
|PM|2=|x-4|2,|FM|2=32+y2=12-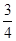 x2.
x2.
①若|PF|=|FM|,则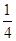 (x-4)2=12-
(x-4)2=12-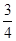 x2,解得x=-2或x=4(舍去),x=-2时,P(-2,0),此时P,F,M三点共线,不合题意.∴|PF|≠|FM|;
x2,解得x=-2或x=4(舍去),x=-2时,P(-2,0),此时P,F,M三点共线,不合题意.∴|PF|≠|FM|;
②若|PM|=|PF|,则(x-4)2=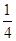 (x-4)2,解得x=4,不合题意;
(x-4)2,解得x=4,不合题意;
③若|PM|=|FM|,则(x-4)2=12-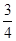 x2,解得x=4(舍去)或x=
x2,解得x=4(舍去)或x=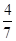 ,x=
,x=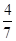 时y=±
时y=±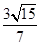 ,
,
∴P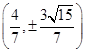 .
.
综上可得,存在点P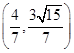 或
或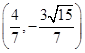 ,使得△FPM为等腰三角形.
,使得△FPM为等腰三角形.
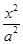 +
+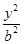 =1,由已知可得2a=4,a=2c,解得a=2,c=1,b2=a2-c2=3.
=1,由已知可得2a=4,a=2c,解得a=2,c=1,b2=a2-c2=3.∴椭圆的标准方程为
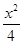 +
+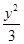 =1,圆的标准方程为(x-1)2+y2=1.
=1,圆的标准方程为(x-1)2+y2=1.(2)设P(x,y),则M(4,y),F(1,0),-2≤x≤2,
∵P(x,y)在椭圆上,∴
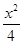 +
+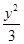 =1,
=1,∴y2=3-
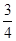 x2.
x2.∴|PF|2=(x-1)2+y2=(x-1)2+3-
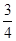 x2=
x2=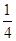 (x-4)2,
(x-4)2,|PM|2=|x-4|2,|FM|2=32+y2=12-
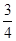 x2.
x2.①若|PF|=|FM|,则
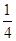 (x-4)2=12-
(x-4)2=12-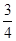 x2,解得x=-2或x=4(舍去),x=-2时,P(-2,0),此时P,F,M三点共线,不合题意.∴|PF|≠|FM|;
x2,解得x=-2或x=4(舍去),x=-2时,P(-2,0),此时P,F,M三点共线,不合题意.∴|PF|≠|FM|;②若|PM|=|PF|,则(x-4)2=
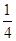 (x-4)2,解得x=4,不合题意;
(x-4)2,解得x=4,不合题意;③若|PM|=|FM|,则(x-4)2=12-
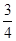 x2,解得x=4(舍去)或x=
x2,解得x=4(舍去)或x=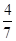 ,x=
,x=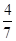 时y=±
时y=±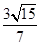 ,
,∴P
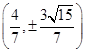 .
.综上可得,存在点P
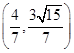 或
或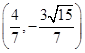 ,使得△FPM为等腰三角形.
,使得△FPM为等腰三角形.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
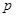 :方程
:方程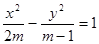 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆;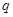 :双曲线
:双曲线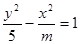 的离心率
的离心率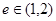 ,若
,若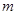 的取值范围.
的取值范围.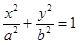 (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线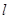 与椭圆C交于不同两点M,N.
与椭圆C交于不同两点M,N. 的长;
的长; 表示的曲线为椭圆,则
表示的曲线为椭圆,则 的取值范围是( )
的取值范围是( )



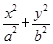 =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( ) =1
=1 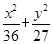 =1
=1  =1
=1  =1
=1 .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积.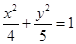 的一个焦点坐标是( )
的一个焦点坐标是( )
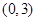

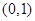
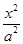 +
+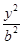 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=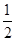 ,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )
,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )


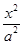 +
+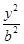 =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=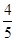 ,则C的离心率为________.
,则C的离心率为________.