题目内容
【题目】已知 ![]() ,
, ![]() ,向量
,向量 ![]() ,
, ![]() 的夹角为90°,点C在AB上,且∠AOC=30°.设
的夹角为90°,点C在AB上,且∠AOC=30°.设 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),求
(m,n∈R),求 ![]() 的值.
的值. 
【答案】解: ![]() ,
, ![]() ,向量
,向量 ![]() ,
, ![]() 的夹角为90°,点C在AB上,且∠AOC=30°,
的夹角为90°,点C在AB上,且∠AOC=30°,
∴在直角三角形ABC中,B=30°,∠COB=60°,∴OC⊥AB,
则△AOC,△BOC都是直角三角形,
则 OC=OAsin60°= ![]() ,
,
在方程 ![]() =m
=m ![]() +n
+n ![]() 两边同乘以向量
两边同乘以向量 ![]() 、
、 ![]() 得:
得: 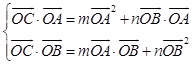 ,
,
即 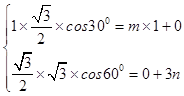 ,∴
,∴ 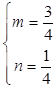 ,∴
,∴ ![]() 的值为3.
的值为3.
【解析】可得,∠COB=60°,OC⊥AB,△AOC,△BOC都是直角三角形,则 OC=OAsin60°= ![]() ,在方程
,在方程 ![]() =m
=m ![]() +n
+n ![]() 两边同乘以向量
两边同乘以向量 ![]() 、
、 ![]() 得
得 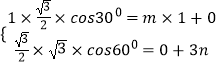 ,可得
,可得 ![]() 的值为3.
的值为3.
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?