题目内容
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
.
(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点D到平面PAC的距离.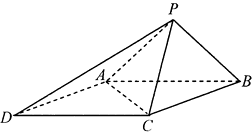
【答案】(Ⅰ)证明:取AB的中点O,连接PO,CO,AC, 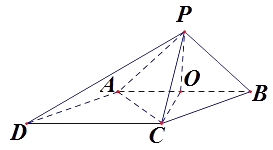
∵△APB为等腰三角形,∴PO⊥AB
又∵四边形ABCD是菱形,∠BCD=120°,
∴△ACB是等边三角形,∴CO⊥AB
又CO∩PO=O,∴AB⊥平面PCO,
又PC平面PCO,∴AB⊥PC.
(II)解:∵∠APB=90°,AB=2,AP=BP= ![]() ,∴PO=1
,∴PO=1
∵△ABC是边长为2的正三角形,
∴OC= ![]()
又PC=2,
∴PO2+CO2=PC2 ,
∴PO⊥OC,
又PO⊥AB,AB∩OC=O,
∴PO⊥平面ABC,
∵四边形ABCD是菱形,
∴B,D到平面PAC的距离相等,设为h,
∵S△PAC= 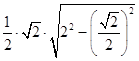 =
= ![]() ,S△ABC=
,S△ABC= ![]() .
.
∴由VB﹣PAC=VP﹣ABC , 可得 ![]() ,
,
∴h= ![]() .
.
【解析】(Ⅰ)取AB的中点O,连接PO,CO,AC,由已知条件推导出PO⊥AB,CO⊥AB,从而AB⊥平面PCO,由此能证明AB⊥PC.(Ⅱ)由VB﹣PAC=VP﹣ABC , 求点D到平面PAC的距离.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则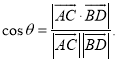 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目

