题目内容
【题目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= ![]()
![]() ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间.
【答案】
(1)解:已知: ![]() ,
, ![]() ,
,
则: ![]() =msin2x+ncos2x,
=msin2x+ncos2x,
y=f(x)的图象过点y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
则: 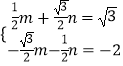 解得:
解得: ![]() ,
,
即:m= ![]() ,n=1
,n=1
故答案为: m= ![]() ,n=1
,n=1
(2)解:由(1)得: ![]() =
= ![]() ,f(x)向左平移φ个单位得到:
,f(x)向左平移φ个单位得到:
g(x)=2sin(2x+2Φ+ ![]() ),
),
设g(x)的对称轴x=x0,最高点的坐标为:(x0,2)点(0,3)的距离的最小值为1,则: ![]() ,
,
则:g(0)=2,
解得:Φ= ![]() ,
,
所以:g(x)=2sin(2x+ ![]() )=2cos2x.
)=2cos2x.
令:﹣π+2kπ≤2x≤2kπ (k∈Z)
则:单调递增区间为:[ ![]() ](k∈Z)
](k∈Z)
故答案为:单调递增区间为:[ ![]() ](k∈Z)
](k∈Z)
【解析】(1)首先根据向量的数量积的坐标运算求得f(x)=msin2x+ncos2x,进一步根据图象经过的点求得:m和n的值.(2)由(1)得: ![]() =
= ![]() ,f(x)向左平移φ个单位得到g(x)=2sin(2x+2Φ+
,f(x)向左平移φ个单位得到g(x)=2sin(2x+2Φ+ ![]() )设g(x)的对称轴x=x0 , 最高点的坐标为:(x0 , 2)点(0,3)的距离的最小值为1,则:g(x)=2sin(2x+
)设g(x)的对称轴x=x0 , 最高点的坐标为:(x0 , 2)点(0,3)的距离的最小值为1,则:g(x)=2sin(2x+ ![]() )=2cos2x,进一步求得单调区间.
)=2cos2x,进一步求得单调区间.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案