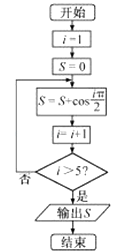
题目内容
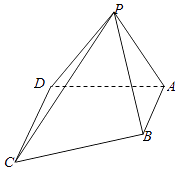
【题目】如图,在四棱锥P﹣ABCD中, ![]() 平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,
平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形, ![]() .
. 
(1)证明:平面PAB⊥平面PCD;
(2)若三棱锥B﹣PAD的体积为 ![]() ,求平面PAD与平面PBC所成二面角的余弦值.
,求平面PAD与平面PBC所成二面角的余弦值.
【答案】
(1)证明:依题: ![]() CD⊥面PADCD⊥AP,
CD⊥面PADCD⊥AP,
又AP⊥PD,∴AP⊥平面PCD,
又AP平面PAB,∴平面PAB⊥平面PCD;
(2)解:  AB∥CD
AB∥CD
由(1)知AB⊥面PAD∴ ![]() =
= ![]() ,
,
取AD中点O,PO⊥AD,平面PAD平面ABCD,∴PO平面ABCD,
以过点O且平行于AB的直线为x轴,如图建系,各点坐标如图.
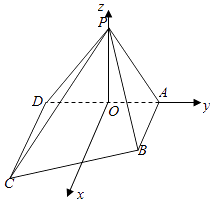
由(1)易知平面PAD的一法向量为 ![]() ,
,
设平面PBC的法向量为 ![]()
. ![]() ,
, ![]() .
. 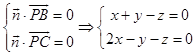 ,
,
取x=2, ![]() .
. ![]() =
= 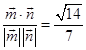 ,
,
故所求二面角的余弦值为 ![]() .
.
【解析】(1)依题意得CD⊥AP,AP⊥PD,即AP⊥平面PCD,可得平面PAB⊥平面PCD(2) ![]() ,AB∥CD
,AB∥CD
由(1)知AB⊥面PAD,由 ![]() =
= ![]() ,
,
取AD中点O,以过点O且平行于AB的直线为x轴建系,利用向量求解.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目