题目内容
【题目】某手机商家为了更好地制定手机销售策略,随机对顾客进行了一次更换手机时间间隔的调查.从更换手机的时间间隔不少于3个月且不超过24个月的顾客中选取350名作为调查对象,其中男性顾客和女性顾客的比为![]() ,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
事件间隔(月) |
|
|
|
|
|
|
|
男性 | x | 8 | 9 | 18 | 12 | 8 | 4 |
女性 | y | 2 | 5 | 13 | 11 | 7 | 2 |
(1)计算表格中x,y的值;
(2)若以频率作为概率,从已抽取的105且更换手机时间间隔为3至6个月(含3个月和6个月)的顾客中,随机抽取2人,求这2人均为男性的概率;
(3)请根据频率分布表填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“频繁更换手机与性别有关”.
以上的把握认为“频繁更换手机与性别有关”.
频繁更换手机 | 未频繁更换手机 | 合计 | |
男性顾客 | |||
女性顾客 | |||
合计 |
附表及公式:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
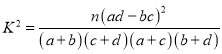
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)填表见解析;没有
(3)填表见解析;没有![]() 以上的把握认为“频繁更换手机与性别有关”
以上的把握认为“频繁更换手机与性别有关”
【解析】
(1)由抽样总数乘以男性与女性分别的比例,得到分别样本的总数,再由分层抽样的比例构建方程求得各自应抽取的样本数,进而在表中分别减去其他各组的数据,求得x与y;
(2)由(1)可知更换手机时间间隔为3至6个月(含3个月和6个月)的顾客中男性与女性的人数,分别设男性分别为a,b,c,d,女性分别为e,f,写出从中抽取两人的所有基本事件,得到总数,再选取均为男性的基本事件,得到此类数量,由古典概型概率计算得答案;
(3)由题意完成![]() 列联表,由公式计算
列联表,由公式计算![]() 的观测值,并与6.635比较大小,即可说明.
的观测值,并与6.635比较大小,即可说明.
(1)由题知男性顾客共有![]() 人,
人,
女性顾客共有![]() 人,
人,
按分层抽样抽取105人,则应该抽取男性顾客![]() 人,
人,
女性顾客![]() 人;
人;
所以![]() ,
,
![]() ;
;
(2)记“随机从已抽取的105名且更换手机时间间隔为3至6个月(含3个月和6个月)的顾客中,
抽取2人”为事件A,设男性分别为a,b,c,d,女性分别为e,f,
则事件A共包含![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 15个可能结果,
15个可能结果,
其中2人均男性有![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 6种可能结果,
6种可能结果,
所以2人均是男性的概率为![]() ;
;
(3)由频率分布表可知,在抽取的105人中,男性顾客中频繁更换手机的有21人,女性顾客中频繁更换手机的有9人,据此可得![]() 列联表:
列联表:
频繁更换手机 | 未频繁更换手机 | 合计 | |
男性顾客 | 21 | 42 | 63 |
女性顾客 | 9 | 33 | 42 |
合计 | 30 | 75 | 105 |
所以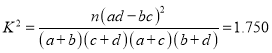 ;因为
;因为![]()
所以没有![]() 以上的把握认为“频繁更换手机与性别有关”.
以上的把握认为“频繁更换手机与性别有关”.