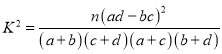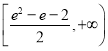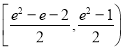题目内容
【题目】如图,PO垂直圆O所在的平面,AB是圆O的一条直径,C为圆周上异于A,B的动点,D为弦BC的中点,![]() ,
,![]() .
.
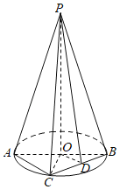
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当四面体PABC的体积最大时,求B到平面PAC的距离.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)由题意可知![]() ,根据圆的几何性质可知
,根据圆的几何性质可知![]() ;由中位线定理可得
;由中位线定理可得![]() ,
,![]() 即可证明
即可证明
(2)根据题意可知当![]() 时,四面体PABC的体积最大,取线段AC的中点E,连接OE,PE,可由勾股定理求得
时,四面体PABC的体积最大,取线段AC的中点E,连接OE,PE,可由勾股定理求得![]() ,进而求得
,进而求得![]() ,再根据等体积法即可求得B到平面PAC的距离.
,再根据等体积法即可求得B到平面PAC的距离.
(1)证明:因为PO垂直圆O所在平面,所以![]() .
.
![]() 是圆O的一条直径,
是圆O的一条直径,
则![]() ,即
,即![]()
因为D为弦BC的中点,O为圆O的圆心,
则![]()
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
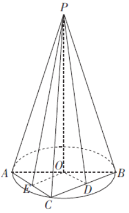
(2)当![]() 时,四面体PABC的体积最大,
时,四面体PABC的体积最大,
此时![]() .
.
取线段AC的中点E,连接OE,PE,则![]() ,
,![]() ,
,![]() ,从而
,从而![]() .
.
设B到平面PAC的距离为h,由![]() ,得
,得![]() ,
,
解得![]() ,即B到平面PAC的距离为
,即B到平面PAC的距离为![]() .
.

【题目】某理财公司有两种理财产品![]() 和
和![]() ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
投资结果 | 获利20% | 获利10% | 不赔不赚 | 亏损10% |
概率 | 0.2 | 0.3 | 0.2 | 0.3 |
产品![]() (其中
(其中![]() )
)
投资结果 | 获利30% | 不赔不赚 | 亏损20% |
概率 |
| 0.1 |
|
(1)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求
进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求![]() 的取值范围;
的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪种产品?
之中选其一,应选用哪种产品?
【题目】某手机商家为了更好地制定手机销售策略,随机对顾客进行了一次更换手机时间间隔的调查.从更换手机的时间间隔不少于3个月且不超过24个月的顾客中选取350名作为调查对象,其中男性顾客和女性顾客的比为![]() ,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
事件间隔(月) |
|
|
|
|
|
|
|
男性 | x | 8 | 9 | 18 | 12 | 8 | 4 |
女性 | y | 2 | 5 | 13 | 11 | 7 | 2 |
(1)计算表格中x,y的值;
(2)若以频率作为概率,从已抽取的105且更换手机时间间隔为3至6个月(含3个月和6个月)的顾客中,随机抽取2人,求这2人均为男性的概率;
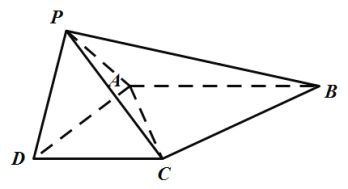
(3)请根据频率分布表填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“频繁更换手机与性别有关”.
以上的把握认为“频繁更换手机与性别有关”.
频繁更换手机 | 未频繁更换手机 | 合计 | |
男性顾客 | |||
女性顾客 | |||
合计 |
附表及公式:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |