题目内容
【题目】在△ABC中,已知![]() ,
, ![]() ,
,![]() ,D是边AC上的一点,将△ABC沿BD折叠,得到三棱锥A-BCD,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设BM=x,则x的取值范围是( )
,D是边AC上的一点,将△ABC沿BD折叠,得到三棱锥A-BCD,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设BM=x,则x的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
折叠前在图1中,![]() ,垂足为
,垂足为![]() ,设图1中
,设图1中![]() 点在
点在![]() 上的射影为
上的射影为![]() ,运动点
,运动点![]() 并加以观察,可得当
并加以观察,可得当![]() 点与
点与![]() 点无限接近时,点
点无限接近时,点![]() 与点
与点![]() 无限接近,所以
无限接近,所以![]() ,在图2中根据斜边大于直角边,可得
,在图2中根据斜边大于直角边,可得![]() ,所以
,所以![]() ,最后在
,最后在![]() 中,利用余弦定理算出
中,利用余弦定理算出![]() ,然后在
,然后在![]() 中算出
中算出![]() ,可得答案.
,可得答案.
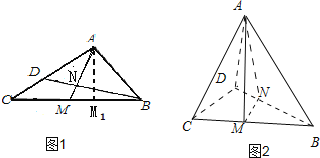
∵将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,且点
,且点![]() 在底面
在底面![]() 的射影
的射影![]() 在线段
在线段![]() 上,
上,
∴在图2中,![]() 平面
平面![]() ,
,![]() 、
、![]() 都与
都与![]() 垂直
垂直
因此,折叠前在图1中,![]() ,垂足为
,垂足为![]() .
.
在图1中过![]() 作
作![]() 于
于![]() ,
,
运动点![]() 可得当
可得当![]() 点与
点与![]() 点无限接近时,折痕
点无限接近时,折痕![]() 接近
接近![]() ,此时
,此时![]() 与点
与点![]() 无限接近;
无限接近;
在图2中,由于![]() 是
是![]() 的斜边,
的斜边,![]() 是直角边,所以
是直角边,所以![]() .
.
由此可得:![]() ,
,
∵![]() 中,
中,![]() ,
, ![]() ,
,![]() ,,
,,
∴![]() ,可得
,可得![]() ,
,
由此可得![]() 中,
中,![]() ,
,
∴![]() ,由
,由![]() 可得
可得![]() 的取值范围为
的取值范围为![]() ,故选C.
,故选C.

【题目】随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
甲班 2 9 1 0 8 2 | 18 17 16 | 乙班 0 0 1 4 7 3 |
(1)判断哪个班的平均身高较高, 并说明理由;
(2)计算甲班的样本方差;
(3)现从乙班这6名学生中随机抽取两名学生,求至少有一名身高不低于![]() 的学生被抽中的概率.
的学生被抽中的概率.
【题目】某农科所对冬季昼夜温差![]() (
(![]() )与某反季节新品种大豆种子的发芽数(颗)之间的关系进行分析研究,他们分别记录了12月1日至12月5日每天的昼夜温差与实验室每天每100颗种子的发芽数,得到的数据如下表所示:
)与某反季节新品种大豆种子的发芽数(颗)之间的关系进行分析研究,他们分别记录了12月1日至12月5日每天的昼夜温差与实验室每天每100颗种子的发芽数,得到的数据如下表所示:
12月1日 | 12月2日 | 12月3日 | 12月4日| | 12月5日 | |
| 10 | 11 | 13 | 12 | 8 |
| 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取3组求线性回归方程,剩下的2组数据用于线性回归方程的检验.
(1)请根据12月2日至12月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选的验证数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?如果可靠,请预测温差为14![]() 时种子的发芽数;如果不可靠,请说明理由.
时种子的发芽数;如果不可靠,请说明理由.
参考公式: