题目内容
【题目】已知椭圆![]() ,圆
,圆![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,与圆相切与
两点,与圆相切与![]() 点,且
点,且![]() 为线段
为线段![]() 的中点,若这样的直线
的中点,若这样的直线![]() 有4条,则
有4条,则![]() 的取值范围为______.
的取值范围为______.
【答案】![]()
【解析】
分直线斜率存在和不存在两种情况各两条,![]() 根据中点弦和切线关系解出中点坐标,再根据点
根据中点弦和切线关系解出中点坐标,再根据点![]() 在椭圆内部即可解得
在椭圆内部即可解得![]() 的取值范围.
的取值范围.
根据椭圆和圆的对称性,要使这样的直线有4条,必斜率不存在的直线两条,且斜率存在的直线两条,
(i)当直线斜率不存在时,要有两条符合题意:![]()
(ii)当直线斜率存在时也有两条直线满足条件才符合题意,当![]() 时,
时,![]() 两条直线符合题意,
两条直线符合题意,
当![]() 时,先证明中点弦公式:直线
时,先证明中点弦公式:直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,则
的中点,则![]()
设![]() 在椭圆上,
在椭圆上,
![]() 为线段
为线段![]() 的中点,
的中点,![]()
![]() ,
,![]() 两式相减:
两式相减:
![]()
![]()
![]()
![]()
当直线斜率存在时,设点![]() ,在圆上
,在圆上![]()
根据中点弦公式![]() ,
,
![]()
根据直线与圆相切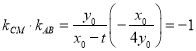
点![]() ,在圆上
,在圆上![]()
解得:![]() ,这样的点
,这样的点![]() 两个,关于x轴对称,
两个,关于x轴对称,
点![]() 在椭圆内部:
在椭圆内部:![]() 即
即![]()
解得![]() ,
,![]()
综上所述:![]()
故答案为:![]()

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响.经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表

摄氏温度 | —5 | 4 | 7 | 10 | 15 | 23 | 30 | 36 |
热饮杯数 | 162 | 128 | 115 | 135 | 89 | 71 | 63 | 37 |
(参考公式) ,
,
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() .样本中心点为
.样本中心点为![]() .
.
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里.因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少.统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱.请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱.请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(1)中求出的线性回归方程
.对于(1)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?