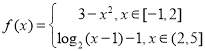题目内容
【题目】从![]() 中任取
中任取![]() 个数,从
个数,从![]() 中任取
中任取![]() 个数,
个数,
(1)能组成多少个没有重复数字的四位数?
(2)若将(1)中所有个位是![]() 的四位数从小到大排成一列,则第
的四位数从小到大排成一列,则第![]() 个数是多少?
个数是多少?
【答案】(1) 1260 ;(2) 7205.
【解析】
(1)需要分两类:第一类,不选0时;第二类,选0时,根据分类计数原理可得;
(2)先分5种情况,形如①“1××5",②"2××5",③“3××5”,④“4××5”,⑤“6××5”,再寻找规律,问题得以解决.
解:(1)不选0时,有![]() 个;选0时,0不能排在首位,
个;选0时,0不能排在首位, ![]() ,根据分类计数原理,共有720+540=1260个四位数.
,根据分类计数原理,共有720+540=1260个四位数.
(2)①“1××5”,中间所缺的两数只能从0,2,4,6中选排,有![]() 个;
个;
②“2××5",中间所缺的两数是奇偶数各一个,有![]() 个;
个;
③“3××5",仿“1××5”,也有![]() 个;
个;
④“4××5",仿“2××5",也有![]() 个;
个;
⑤“6××5”也有![]() 个;
个;
即小于7000的数共有96个,故第97个数是7025,第98个数是7045,第99个数是7065,第100个数是7205.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目