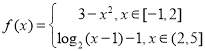Question

【题目】已知，对于，均有，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

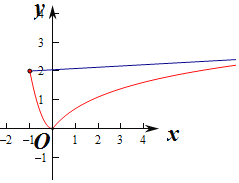
利用条件转化为f（x）≤m（x+1）+2，即f（x）的图象不高于直线y＝m（x+1）+2的图象，求出函数f（x）＝ln（x+1）过点（﹣1，2）的切线方程，利用数形结合进行求解即可．

若x∈[﹣1，+∞），均有f（x）﹣2≤m（x+1），得x∈[﹣1，+∞），均有f（x）≤m（x+1）+2

即f（x）的图象不高于直线y＝m（x+1）+2的图象，直线y＝m（x+1）+2过定点（﹣1，2），

作出f（x）的图象，由图象知f（﹣1）＝2，

设过（﹣1，2）与f（x）＝ln（x+1）（x>0）相切的直线的切点为（a，ln（a+1）），（a>0）

则函数的导数f′（x），即切线斜率k，

则切线方程为y﹣ln（a+1）（x﹣a），

即yxln（a+1），

∵切线过点（﹣1，2），

∴2ln（a+1）＝﹣1+ln（a+1）

即ln（a+1）＝3，

则a+1＝e3，

则a＝e3﹣1，

则切线斜率k

要使f（x）的图象不高于直线y＝m（x+1）+2的图象，

则m≥k，

即实数m的取值范围是[，+∞），

故选：B．